初めに
この記事は下のリンクの記事の補足内容となっております。基礎からしっかり学びたい方や、基本をもう一度復習したい方はぜひ下の記事を読んでからみてください。
また、このサイトは下の本を参考にしています。よかったら買ってみてください。
“基礎から始めたい”という方にお勧めの一冊!!
 | 高校数学Bの解き方をひとつひとつわかりやすく。 (高校ひとつひとつわかりやすく) [ 学研プラス ] 価格:1,210円 |
それでは公式と証明を見ていきましょう‼‼
正規分布の標準化に関する基本公式
正規分布の標準化に関する基本公式です。普通の高校生は覚えるだけで終わってしまっていますが、これは結構重要な公式なので、しっかり、証明も押さえておきましょう。
確率変数Xが、正規分布N(m,σ²)に従うとき、Z=(X-m)/σと置くと、確率変数Zは、標準正規分布N(0,1)に従います。
このことを正規分布の標準化とも言います。
この公式の証明をしていきます。
講師は全員京大生だから安心正規分布の標準化に関する基本公式の証明
これを証明する前に、まず、下の公式を証明しておきます。
確率変数Xが正規分布N(m,σ²)に従うとき、Xを1次式で変換してできる確率変数aX+bは正規分布N(am+b,a²σ²)に従う。
これは下のように積分を使って求めることができます。

↑裏の赤がちょっと移ってしまっていますがそれは気にしないでください。

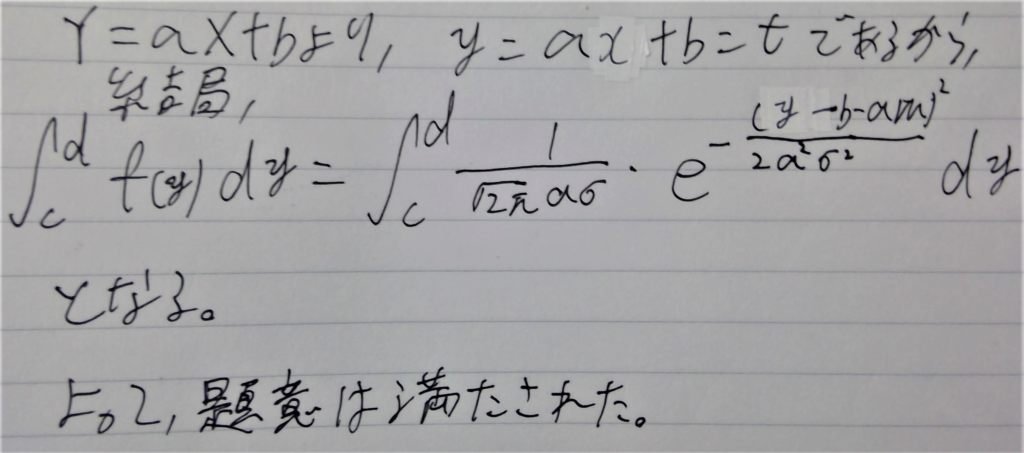
これで証明完了です。あとは、これの、aに1/σを、bに-m/σを、代入することで、上の公式が導かれます。
終わりに
二項分布の範囲以外の確率・統計分野についてもっと知りたい方は、ぜひ、下のリンクの記事を読んでください。
ほかにも面白い記事がたくさんありますので、そちらのほうも見ていただければ光栄です。
それでは次の記事で‼‼




プロフィール
このブログの情報が少しでも役に立てれば嬉しいです。