【目指せ本選‼】超わかりやすい日本数学オリンピック予選2021全問解説

初めに

前回に引き続き数学オリンピック予選2021の解説をしていこうと思います‼‼

本記事では問5から問8までなので、ほかの問題の解説が気になる方は、下のリンクをクリック‼‼

また、この記事の最後のほうでは、「数学オリンピックの問題を解けるようになる方法」について解説しているので、そちらに興味がある方は、この記事の最後のほうをチェック‼‼

【超わかりやすい‼‼】数学オリンピック予選2021全問解説‼

数学オリンピック予選2021の問題を全問解説していこうと思います‼‼わからない問題があった方や、解説を読んでも意味が分からなかった方は、誰でも簡単にわかるように超わかりやすく解説しているので、ぜひ読んでみてください。ちなみに、この記事では数学オリンピック2021予選の問1、問2、問3、問4を解説します。

information-station.work

＼良問揃い‼／JMO予選2021全問解説‼‼

数学オリンピック予選2021の問題を全問解説していこうと思います‼‼わからない問題があった方や、解説を読んでも意味が分からなかった方は、誰でも簡単にわかるように超わかりやすく解説しているので、ぜひ読んでみてください。ちなみに、この記事では数学オリンピック2021予選の問9、問10、問11、問12を解説します。

information-station.work

それでは、日本数学オリンピック予選2021の問題の解答・解説を見ていきましょう‼‼

問5:

問題：下の図のように一辺の長さが1の立方体4個からなるブロックが4種類ある。このようなブロック4個を2×2×4の直方体にはみ出さないように敷き詰める方法は何通りあるか？ただし、ブロック同士は区別するものとし、回転させて一致する入れ方は異なるものとして数える。

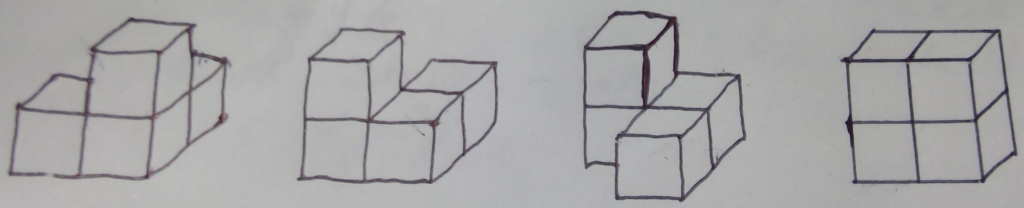
解説:まず、左から順にa,b,c,dとする。

この時a,b,c,dどの相異なる二つのブロックをとってもうまく組み合わさらない(はみ出したり、余ったりする)ため、a,b,c,dは必ずそれぞれのブロックとくっつくことで、2×2×2の立方体となります。

ここで、aどうして作る立方体については4通り、bについては6通り、cについても6通りです。

よって、2×2×2の立方体が2つあるときは、dが2×2×2の立方体を作る場合における通り数は3通りであるから、(4+6+6+3)^2=361通り、2×2×2の立方体が一つでdが二つ(上側と下側)ある時は、(4+6+6+3)×1-1=18通り(-1は全部dの時)であるから、求める通り数は361+18=379通り。

これは解き方はとても簡単ですが計算ミスや数え間違いがしやすい問題です。数学オリンピックの5番としては簡単だと思います。

問6:

問題:正の整数nに対して、正の整数mであって、mとnが互いに素であり、m+1とn+1が互いに素であるもののうち最小のものをf(n)と表す。この時、f(1),f(2),…,f(10^10)のうちに現れる正の整数は何個あるか？

解答・解説：n+1を割り切らない素数のうち、最小のものをpとする。

もしf(n)<=p-1とする。この時、n+1互いに素でない整数qを用いて、f(n)=q-1<p-1と表すことができる。

しかし、この場合、n+1とm+1が互いに素にならないため矛盾。よってf(n)>=p-1である。

　ここではf(n)=p-1の時について考える。f(n)=m=p-1の時、m+1=pは仮定より、明らかにn+1と互いに素である。

また、仮定より、n+1は確実にp以下の素因数はすべて持つから、p-1の任意の素因数はすべて持つ。

ここで、n+1とnは互いに素であるからn+1が持っている素因数は絶対にnは持たない。よって、nが持っている素因数も絶対nは持たないから、nとmは互いに素である。よってf(n)=p-1であることが導かれた。

　次に、pの最大は31であるから、(2から順に素数をかけていって10^10+1ぎりぎりになる数は29なのでpはその一つ上の素数である31が最大です。)よって、31以下の素数の個数を調べて、答えは11とわかります。

説明は長くなってしまいましたがいろいろ試していくと、こんなことしなくても、「規則性はこんな感じかな」わかるので、解くときは最後にミスさえしなかったら、この問題で詰まったり、間違えたりすることはそこまでないと思います。

問7:

三角形ABCの辺BC上に点P,Qがあり、三角形ACPとABQの垂心は一致している。AB=10,AC=11,BP=5,CQ=6の時、辺BCの長さをもとめよ。

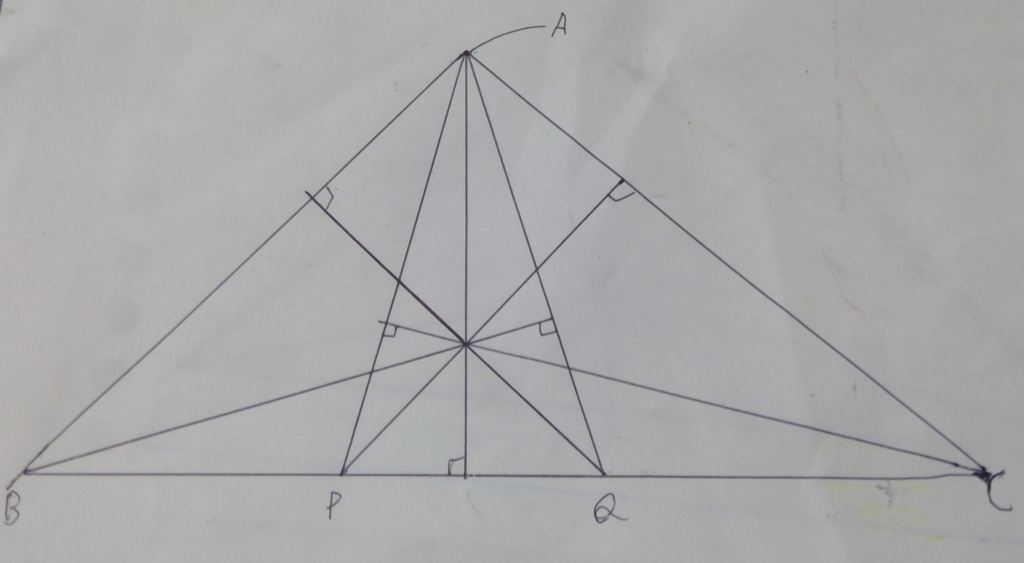
解説:「これは垂心いっぱいあるから⊿ABCの垂心も作っちゃえ」と思えるかがミソです。

まず下の図のように⊿ABCの垂心Hを取り、ほかの点を下の図のように定めます。

すると、下の図のように平行が分かってくるから、5:PR=BP:PR=5:PR=HO:OR=QC:RQ=QC:6と分かるから、PR:RQ=5:6と分かります。
　　　　　　　　

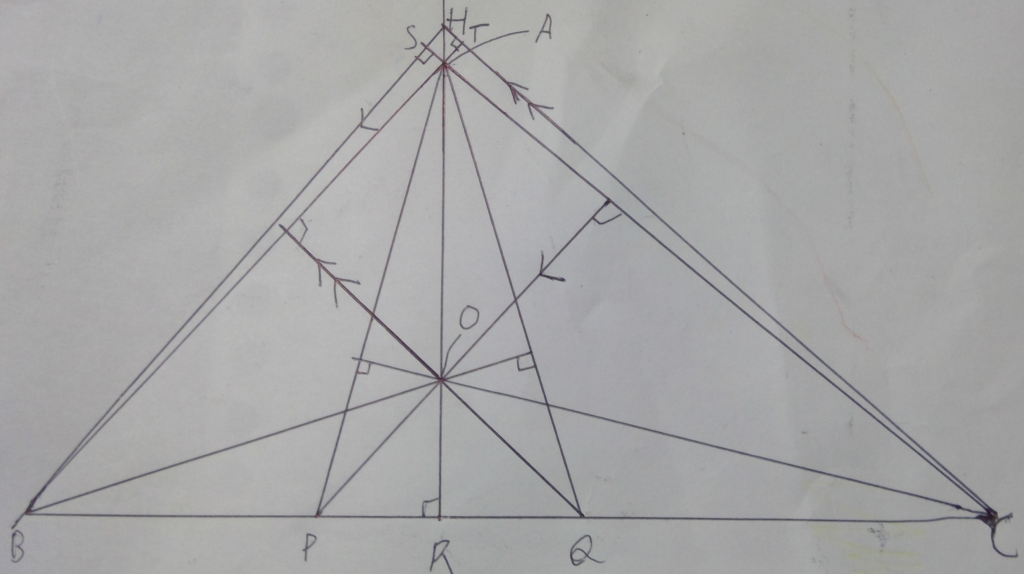
ここでAD=5k,DB=6kと置くと、⊿ABD及び⊿ACDに注目して、三平方の定理より、11k^2=21であるから、k>0より、BCの長さは√231であることが分かります。
　この問題は、もしPQが逆になるような図形を描いたとしても、PQの長さが負になるようにして解いたら答えは一つに定まります。

問8:

2以上20以下の整数の組(a1,a2,a3,…,a17)であって、a1^a2^a3^…^a17≡a2^a3^a4…^a17≡1(mod17)となるものの個数を求めよ。

解説:a₁≡0(mod17)の時は明らかに、
a₁^a₂^a₃^…^a₁₇≡1(mod17)を満たさず、a₁≡1(mod17)の時は明らかに
a₁^a₂^a₃^…^a₁₇≡1(mod17)を満たす。

　a₁>=2(mod17)とする。

フェルマーの小定理よりpが16の倍数の時は、a₁^p≡1(mod17)を満たします。これより、a₂は偶数であることがわかります。

また、もし左の合同式がpが16の倍数以外で、成立したとします。

この時の指数の最小をqとします。この時、qは16以下だと指定することができます。（もし16より大きかったら16を引けばいいだけだから。）すると、qは1でないことに注意してa₁¹⁶≡a₁^qs+r≡1(mod17)(r<=q)とあらわすことができます。

しかしこの時、a₁^r≡1(mod17)となり、r=qとなるため、qは16の約数であることがわかります（1以外）。これにより、どんな場合についても、pは偶数であることがわかるため、a₂が偶数だとわかります。

よってa₁>=2(mod17)の時は、a₃^a₄…^a₁₇が4以上であるから、a₂が偶数であることがa₁^a₂^a₃^…^a₁₇≡1(mod17)を満たすための必要十分条件である。

以上のことより、a₁^a₂^a₃^…^a₁₇≡1(mod17)を満たすための必要十分条件は、a₁≡1(mod17)または、a₂が偶数であることです。

同様のことが、a₂^a₃^a₄…^a₁₇≡1(mod17)の成立条件についてもいえるため、以下のように場合分けをすることができます。

• a₂が偶数の時:　問題の条件を満たすことは、a₁は17とならないため、a₂が18またはa₃が偶数となることと同値であるから、この場合における通り数は、18×(1×19¹⁵+1×8×10×19¹⁴)=1962×19¹⁴通りです。

• a₂が奇数の時:　必然的にa₁≡1(mod17)となるため、a₁=18であり、この時、a₂は奇数であるから、a₂が18にならないため、問題の条件を満たすことはa₃が偶数となることと同値であるから、この場合の通り数は、1×8×10×19¹⁴=80×19¹⁴通りです。

よって求める通り数は二つの場合の通り数を足し合わせることで、2042×19¹⁴通りであることが分かります。

この問題を厳密に証明しようとすると、ここまで長くなってしまいました。

しかし、a₁^p≡1(mod17)を満たすpが16の倍数だけであることは別に証明できなくても、とけてしまうので、答えだけなら分かった方も結構いらっしゃるのではないでしょうか。

いずれにしろ、この問題は合同式の基本的性質を理解するうえでとてもいい問題だったと思います。

数学オリンピックの問題を解けるようになるには

正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか本選の最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。

数学オリンピックの問題を解けるようになるには

正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか本選の最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。

というわけで、数学オリンピック対策でぜひ読んでおくべき本を紹介したいと思います‼‼

下の記事から抜粋しました。もっと詳しく知りたい方は、ぜひ下の記事を読んでください‼

＼受験生必見‼／数学オリンピックの対策法とは？おすすめの参考書や効率的な勉強法を解説‼

「数学オリンピックを受けようと思ったけど、実際どんなふうに手を付けていったらいいかわからない」と思う方は結構いると思います。なので、今回は数学オリンピックで本選あるいは日本代表やメダリストを目指す上でのオススメ参考書や効率的な勉強法を紹介していきたいと思います‼

information-station.work

パーフェクトマスターシリーズ

これは、特定の分野をしっかり固めたい方にお勧めです。

大事な問題だけがセレクトされているので、その分野の問題をしっかり鍛えることができます。

初等整数を鍛えたい方にオススメ‼‼

これは、初等整数をマスターしたい方にお勧めです。

初等整数の問題はよく本選の大門１なんかで出題されることが多いので、そういった類の問題を解けるようになりたい方はこの本がおすすめです‼‼

平面幾何を鍛えたい方にオススメ‼‼

下の本は平面幾何を鍛えたい方にオススメの本です。

「数学オリンピックの幾何の問題を解いていると、「こんな発想が出てくるわけないだろ！！」みたいな問題にあたることはよくあると思います。

この本を読むことで、そういう問題たちをすらすら解けるようになります‼‼

代数・解析を鍛えたい方にオススメ‼‼

下の本は、代数、解析を鍛えたい方におススメの本です

数学オリンピックの問題の中でも、「絶対解けるか！！」みたいなレベルの問題って稀にあるじゃないですか。

こういう問題は、代数・解析の分野に入ることが多いです。

数学オリンピックで、難しい問題を解いてほかの受験生と差をつけたい方にはこの本をお勧めします‼

組み合わせ論を鍛えたい方にオススメ‼‼

下の本は、組み合わせ論を鍛えたい方におススメの本です。

数学オリンピックの場合の数の問題は、ほかの分野に比べてそこまで難しい問題が出題されることはあまりないんですが、とにかくめちゃくちゃミスしやすいように巧妙に仕組まれています。

そんなミスしやすいポイントをしっかり克服するためにも、ぜひこの本は見ていただきたいです。

過去問をひたすら解きまくる

これも結構おすすめです。過去問を全部解いていれば、実質数学オリンピックに関係する問題を全部網羅したようなものなので、完璧にマスターしたい方にはこちらの方法をお勧めします‼‼

ほかにも過去問についてはいろんな著者がいろんな本を出版しているので、ぜひそちらの本も調べてみてください。(下リンク)

Amazon.com

数学オリンピックの参考書は高すぎる‼‼

今紹介させていただいた本を見て思ったかもしれませんが、とにかくこういった類の参考書は高いです。

でも、なんと「kindle Unlimited」なら、今紹介した本が月額980円払うだけでで読むことができます‼‼‼

1冊読むだけで余裕で元を取れますね。

さらに、今だけ初月無料なので、初月だけ契約すれば、本当に1銭も払わず、あの高額な本たちを読むことができます😎

私もこれを使っていて、「kindle Unlimited」なら、大体の本が無料で読めちゃうので、知りたいことがあったら簡単に本で調べたり、本で勉強したりすることができます。

また、息抜きに読書したいときにも役に立つので、ぜひこれは、お勧めしたいです‼‼

↓興味がある方はこちら‼‼

終わりに:

5番から8番はやはり1番から4番に比べて難しいです。(この記事を書くのに1時間ぐらいかかってしまいました。)

ただ、ミスしやすい場所でミスをしないように注意していれば問1から問8で十分合格ラインの6点は余裕でとることができると思います。

また他の問題についての投稿もありますので、それもあわせてお読みおいただければ光栄です。

それでは次の記事で‼