初めに
今回は、数学オリンピック2020の問題の解答・解説をしていきたいと思います‼‼
ノーヒントで解いてみたいという方は、下のリンクをクリック‼‼
第30回(2020年)JMO予選の問題 (imojp.org)
また、この記事の最後に、「数学オリンピックの問題を解けるようになる方法」について解説していますので、興味がある方はそちらのほうも読んでいただければ光栄です。
注意
この記事では、日本数学オリンピック2020の問題のうち、問9から問12までしかしていません。
ほかの問題の解答・解説が気になる方は、下のリンクをクリック‼‼
それでは日本数学オリンピック予選2020の解答・解説を見ていきましょう‼‼
日本数学オリンピック予選2020 解答・解説 問9
問題:
2以上の整数に対して定義され2以上の整数値を取る関数fであって、任意の2以上の整数m,nに対して、
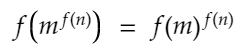
を満たすものを考える。この時、
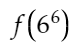
の値を求めよ。
解答・解説:
これも超絶簡単な問題です。
例えば、関数fが、ある整数xに対して、

が成り立つものとします。
この時、先ほどの条件から、
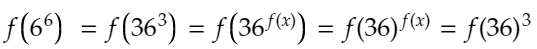
と変形することができます。
これを少し一般化しようと思います。
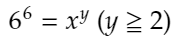
となるようなx,yに対して、関数fが、
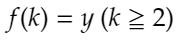
となると仮定することができるので、先ほどの具体例からわかるように、
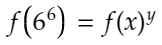
となります。
また、このパターンの時(66をそのまま使うんじゃなくて「何かの累乗」という形にするとき。)は、最小値は、明らかに4と分かります。
よって、
であるため、求める答えは4と分かります。
日本数学オリンピック予選2020 解答・解説 問10
問題:
8×8のマス目を下の図のように白と黒の2色で塗り分ける。黒い駒4個と白い駒4個をそれぞれいずれかのマスに置き、以下の条件を満たすようにする方法は何通りあるか。
- 各行・各列にはちょうど1個の駒が置かれており、黒い駒は黒いマスに、白い駒は白いマスに置かれている。
ただし、同じ色の駒は区別せず、回転や裏返しにより一致する置き方も異なるものとして数える。

解答・解説:
やっぱりまずは試すことが一番だと思います。
黒が黄色で、白が赤で塗っていきたいと思います。


左のやつをちょっといじっただけ。
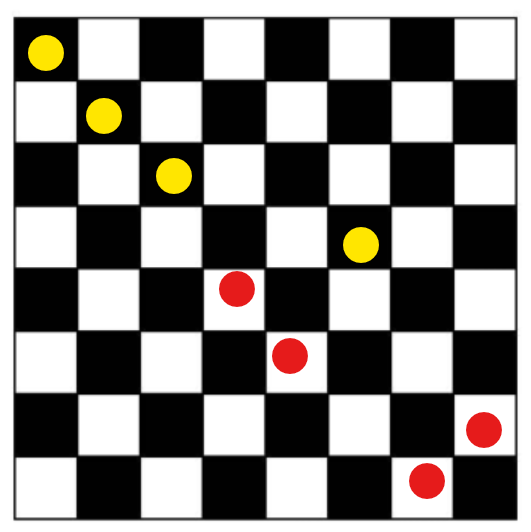
これも一番左のやつをちょっといじっただけ。
もうここらへんで感がいい人は気づいてほしいです。
上の例では、全部一番左のパターンのものを、1箇所だけ変更を加えています。
これを見て、「これを繰り返して言ったら全部のパターンにたどり着くんじゃないの?」という発想に至ることができたら勝ちです。
結局のところ、上の例では、黒い駒は「奇数行奇数列」と「偶数行偶数列」が2個ずつ、白い駒は「奇数行偶数列」と「偶数行奇数列」が2個ずつ存在していることがわかります。
(つまり、黒も白も奇数行と偶数行は2個ずつあるという意味。)
<仮説>上の黄色いアンダーラインで書かれているところのことは上の例だけに限らず一般的に成り立つ。
それでは、この仮説が正しいかどうか検証していってみましょう‼‼
<検証>まず、 「奇数行奇数列」、「偶数行偶数列」、「奇数行偶数列」、「偶数行奇数列」に置いてある駒の数を、それぞれ、x1,1 , x0,0 , x1,0 , x0,1とあらわすことにします。
この時、当たり前ですが、黒いマスにも白いマスにも4個ずつ存在していることから、
- x1,1 + x0,0 = 4
- x1,0 + x0,1 = 4
さらに、各行、各列に1つずつ存在することは分かっているので、
- x1,1 + x1,0 = 4
- x0,0 + x0,1 = 4
- x1,1 + x0,1 = 4
- x0,0 + x1,0 = 4
と分かります。
これにより、x1,1 , x0,0 , x1,0 , x0,1 の値はすべて2と分かるため、仮説が正しかったことがわかります。
よって、縦横ともに4列から2列選んで、そこから2パターン選ぶことで、「偶数行偶数列」といった一つのパターンができるため、これを2回かけて、黒い駒の(白い駒)通り数が確定し、黒い駒の場所が確定した時の通り数は4通りだから、
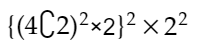
より、答えは、20736通りと分かります。
日本数学オリンピック予選2020 解答・解説 問11
問題:
円Ωの周上に5点A,B,C,D,Pがこの順にある。点Pを通り直線ABに点Aで接する円と点Pを通り直線CDに点Dで接する円がΩの内部の点Kで交わっている。また線分AB,CDの中点をそれぞれM,Nとすると3点A,K,N及びD,K,Mはそれぞれ同一直線上にあった。AK=5,DK=3,KM=7が成り立つとし、直線PKとΩの交点のうちPでない方をQとするとき、線分CQの長さを求めよ。ただし、XYで線分XYの長さを表すものとする。
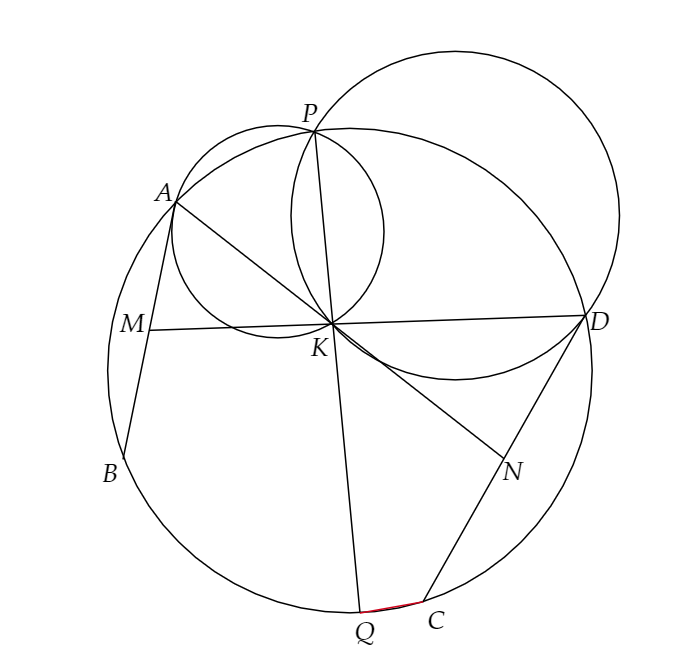
解答・解説:
この問題の一番難しい点は、「いかにして図をきれいに書けるか」です。図さえきれいに書ければこの問題は超簡単に解けます。
まず、接弦定理より、下で示している角度がすべて等しいことがわかります。
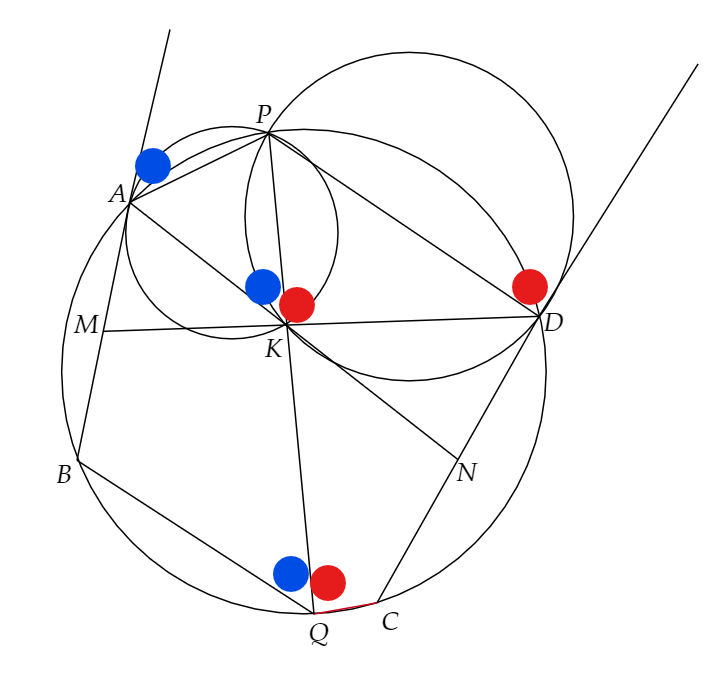
よって、錯覚より下の線が平行になっていることがわかります。
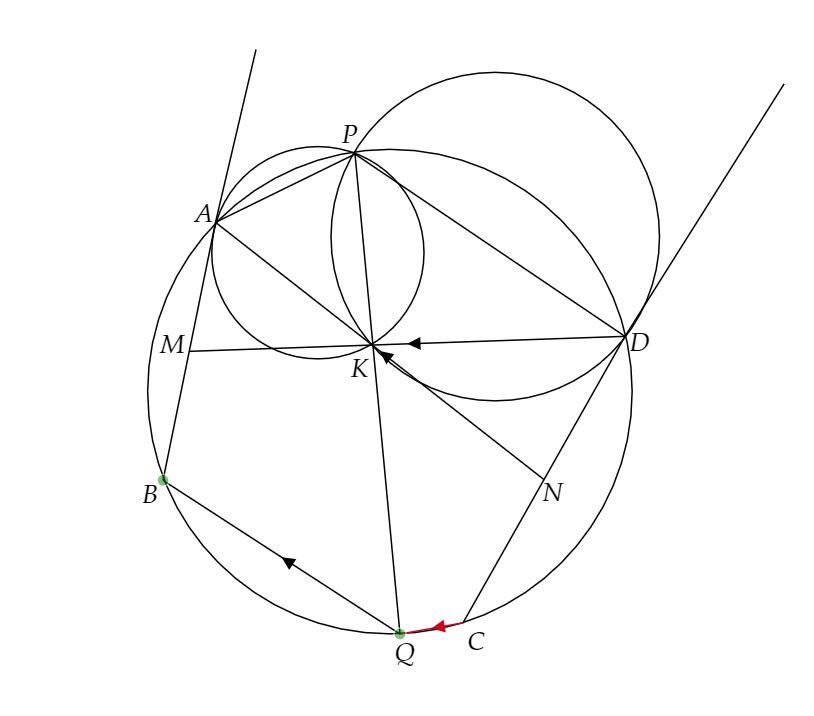
平行の線がせっかく2本もあるし、「中点と平行四辺形は相性がいい」とよく言いますので、平行四辺形を作りたいと思います。
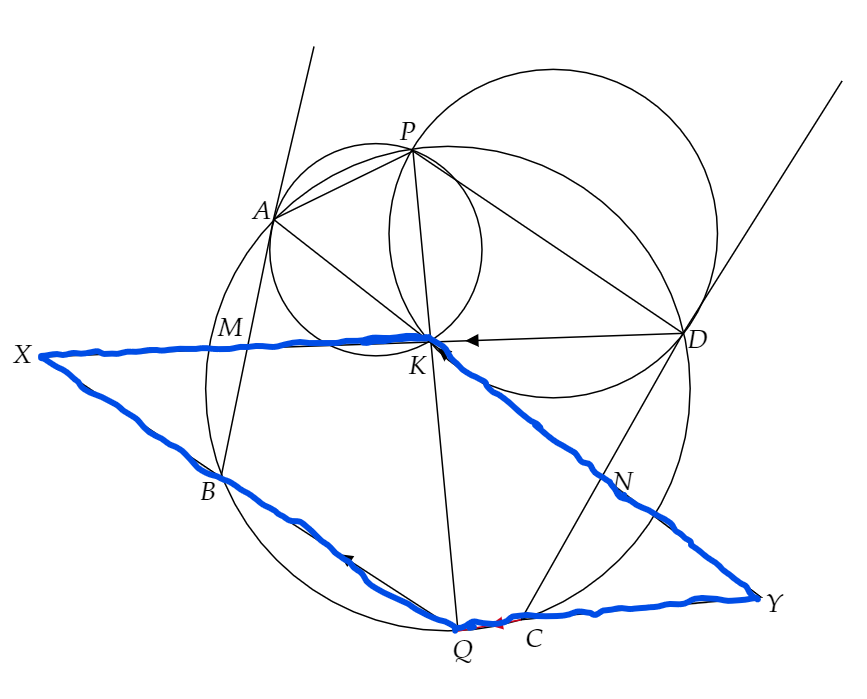
さらに、M,NがAB,CDの中点であることから、下の三角形の合同がわかります。
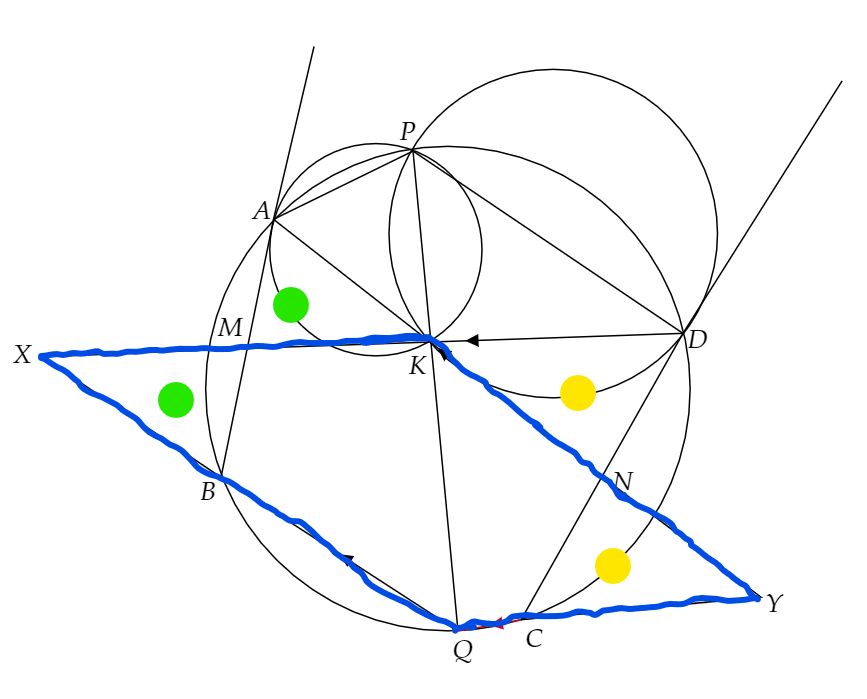
よって、最終的に下のように長さを埋めることができます。
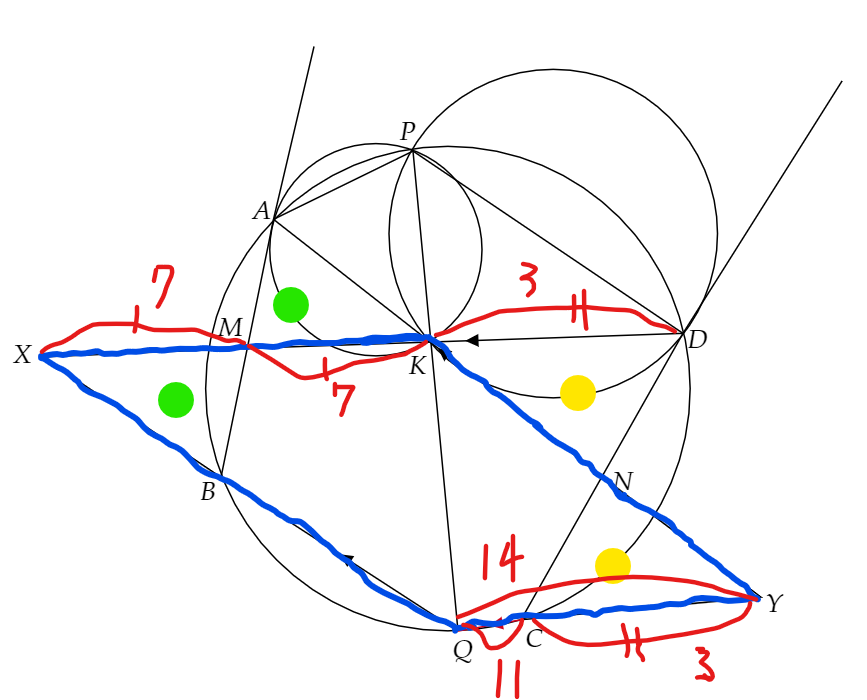
よって、答えは、上の図からわかるように、11です。
日本数学オリンピック予選2020 解答・解説 問12
問題:
正の整数kに対して、k個の正の整数a1,a2…akが次の条件を満たすとき長さkの良い数列と呼ぶことにする。
<条件>
- すべて30以下で相異なる。
- i=1,2…k-1に対し、iが奇数ならば、ai+1は、aiの倍数である。iが偶数ならば、ai+1は、aiの約数である。
よい数列の長さとしてありうる最大の値を求めよ。
解答・解説:
これは、実際にやってみるとわかりやすいです。
適当に7から始めてみましょう。
7,14,2,24,8,16,4,20,5,15,3,27,9,18,6,12,1,22,11
上の数列を見て気付いてほしいことは、「奇数番目の数は10以下」ということです。
見たまんまなので、小学生でもわかります。
結果から言うと「奇数番目の数は10以下」というのには少し語弊があるのですが、なぜ、先ほどのようなことが起きたのか考えてみましょう。
これは、理屈は簡単で、a2,a3,a4のところに注目してみると、
a2とa4のどちらかは×3以上であり、 a2とa4のどちらも30以下なので、必然的にa3は10以下になります。
これを少し一般化すると、「3番目以上で、最後から2番目までのの奇数番目の数は10以下」ということが成り立ちます。
なので、絶対23以下であることがわかります。
また、実際、
13,26,2,14,7,21,3,27,9,18,6,24,8,16,4,20,10,30,5,25,1,26,13
と並べることで、問題の条件を満たす長さが23の数列が存在することが確認できるため、もとめる答えは、23と分かります。
↑これって問1じゃなくて最終問題ですよね…
数学オリンピックの問題を解けるようになるには
正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか本選の最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。
というわけで、数学オリンピック対策でぜひ読んでおくべき本を紹介したいと思います‼‼
パーフェクトマスターシリーズ
これは、特定の分野をしっかり固めたい方にお勧めです。
大事な問題だけがセレクトされているので、その分野の問題をしっかり鍛えることができます。
初等整数を鍛えたい方にオススメ‼‼
これは、初等整数をマスターしたい方にお勧めです。
初等整数の問題はよく本選の大門1なんかで出題されることが多いので、そういった類の問題を解けるようになりたい方はこの本がおすすめです‼‼
平面幾何を鍛えたい方にオススメ‼‼
下の本は平面幾何を鍛えたい方にオススメの本です。
「数学オリンピックの幾何の問題を解いていると、「こんな発想が出てくるわけないだろ!!」みたいな問題にあたることはよくあると思います。
この本を読むことで、そういう問題たちをすらすら解けるようになります‼‼
代数・解析を鍛えたい方にオススメ‼‼
下の本は、代数、解析を鍛えたい方におススメの本です
数学オリンピックの問題の中でも、「絶対解けるか!!」みたいなレベルの問題って稀にあるじゃないですか。
こういう問題は、代数・解析の分野に入ることが多いです。
数学オリンピックで、難しい問題を解いてほかの受験生と差をつけたい方にはこの本をお勧めします‼
組み合わせ論を鍛えたい方にオススメ‼‼
下の本は、組み合わせ論を鍛えたい方におススメの本です。
数学オリンピックの場合の数の問題は、ほかの分野に比べてそこまで難しい問題が出題されることはあまりないんですが、とにかくめちゃくちゃミスしやすいように巧妙に仕組まれています。
そんなミスしやすいポイントをしっかり克服するためにも、ぜひこの本は見ていただきたいです。
過去問をひたすら解きまくる
これも結構おすすめです。過去問を全部解いていれば、実質数学オリンピックに関係する問題を全部網羅したようなものなので、完璧にマスターしたい方にはこちらの方法をお勧めします‼‼
ほかにも過去問についてはいろんな著者がいろんな本を出版しているので、ぜひそちらの本も調べてみてください。(下リンク)
数学オリンピックの参考書は高すぎる‼‼
今紹介させていただいた本を見て思ったかもしれませんが、とにかくこういった類の参考書は高いです。
でも、なんと「kindle Unlimited」なら、今紹介した本が月額980円払うだけでで読むことができます‼‼‼
1冊読むだけで余裕で元を取れますね。
さらに、今だけ初月無料なので、初月だけ契約すれば、本当に1銭も払わず、あの高額な本たちを読むことができます😎
私もこれを使っていて、「kindle Unlimited」なら、大体の本が無料で読めちゃうので、知りたいことがあったら簡単に本で調べたり、本で勉強したりすることができます。
また、息抜きに読書したいときにも役に立つので、ぜひこれは、お勧めしたいです‼‼
↓興味がある方はこちら‼‼
終わりに
いかがでしたか。
ほかにも数学オリンピックの解説している記事もありますので、そちらのほうも見ていただければ光栄です‼‼
それでは次の記事で‼

プロフィール
このブログの情報が少しでも役に立てれば嬉しいです。