初めに
前回に引き続き数学オリンピック予選2021の解説をしていこうと思います‼‼
本記事では問1から問4までなので、ほかの問題の解説が気になる方は、下のリンクをクリック‼‼
また、「数学オリンピックの問題を解けるようになる方法」についてこの記事の最後のほうで解説しているので、そちらに興味がある方は、この記事の最後のところをチェック‼‼
それでは、日本数学オリンピック予選2021の問題の解答・解説を見ていきましょう‼‼
\“プログラミング”が数学力を金に変える‼/
↑必要なのは名前とメアドだけ,顔出し不要,完全オンライン完結‼
問1:
問題:互いに素な正の整数m,nがm+n=90をみたすとき積mnとしてありうる最大の値を求めよ
解説:m,nの差が一番小さくて,かつ,m,nが互いに素であるものをもとめればいいので、mnが最大値となるものはm=43,n=47(順不同)の時で、求める値は、mn=2021
これは数学オリンピックとは思えないくらい簡単でしたね(^^♪
問2:
問題:下の図のような正十角形がある。全体の面積が1の時、斜線部の面積をもとめよ
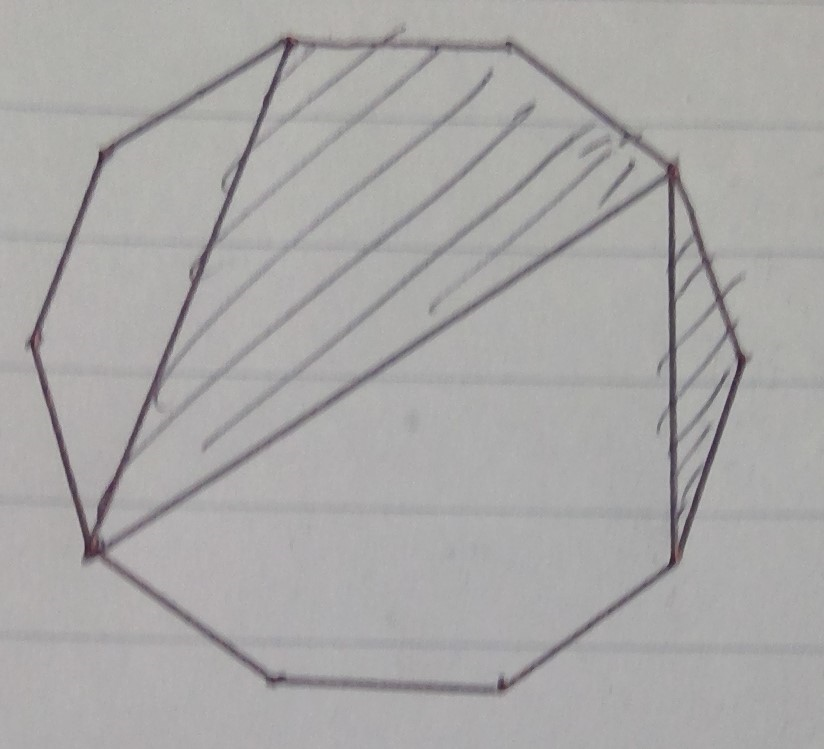
解説:これは個人差が出る問題かと思います。
まず下の図のように小さいやつを移動させます。
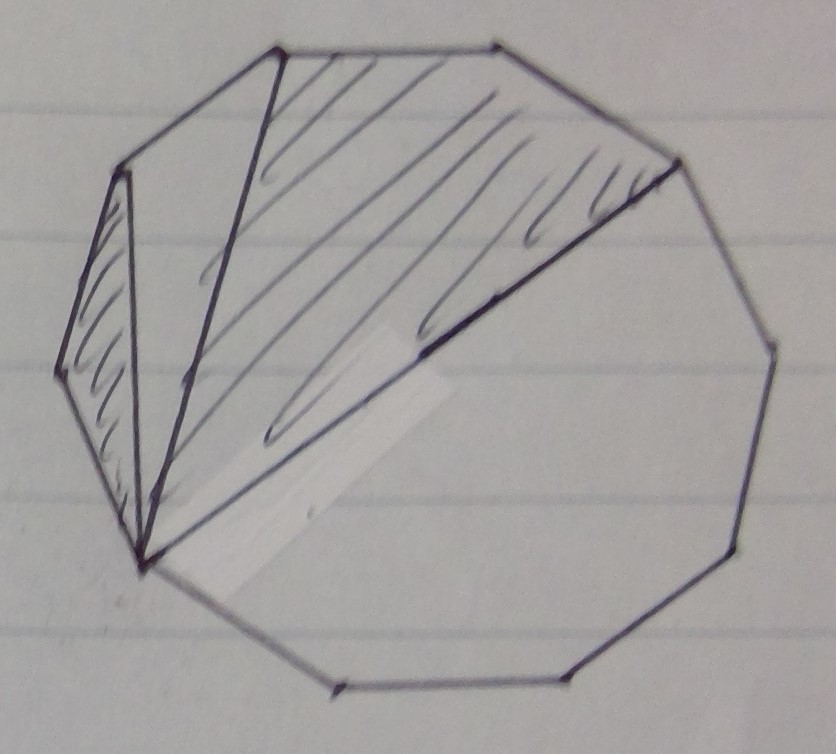
その次に下の図のように等積変形を行います。
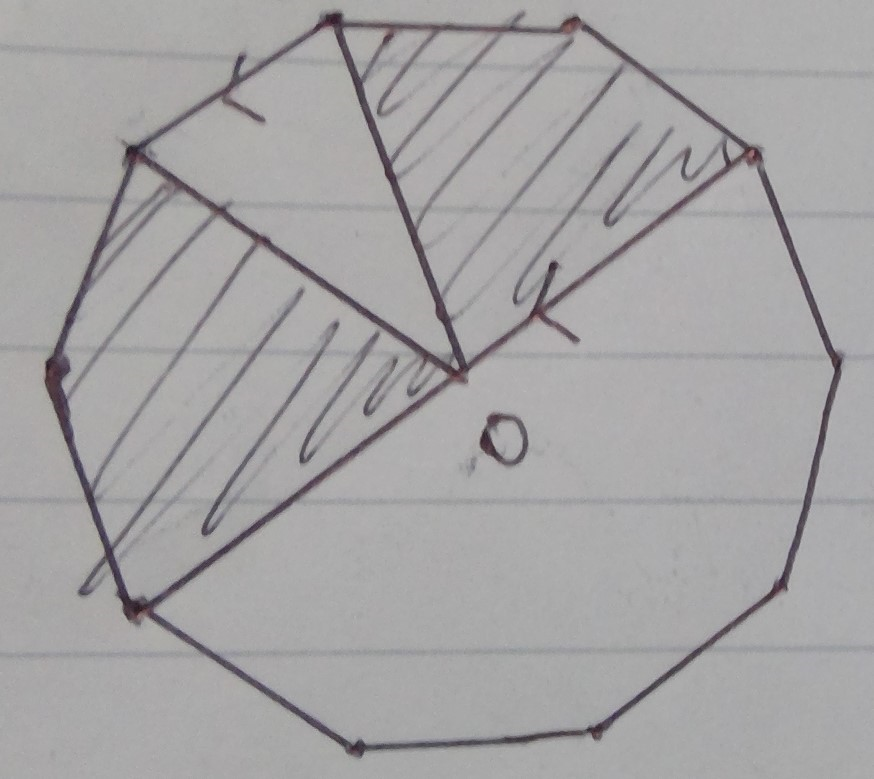
Oを中心とすると1/2から1/10を引けばいいから、よって、求める面積は2/5です。等積変形ができるかどうかがこの問題を解けるかどうかのカギですね。
\“プログラミング”が数学力を金に変える‼/
↑必要なのは名前とメアドだけ,顔出し不要,完全オンライン完結‼
問3:
問題:下の図のようにAB=ACなる二等辺三角形ABCの内部に点Pを取り、PからBC,CA,ABに下した垂線の足をそれぞれD,E,Fとする。BD=9,CD=5,PE=2,PF=5のとき、辺ABの長さをもとめよ。
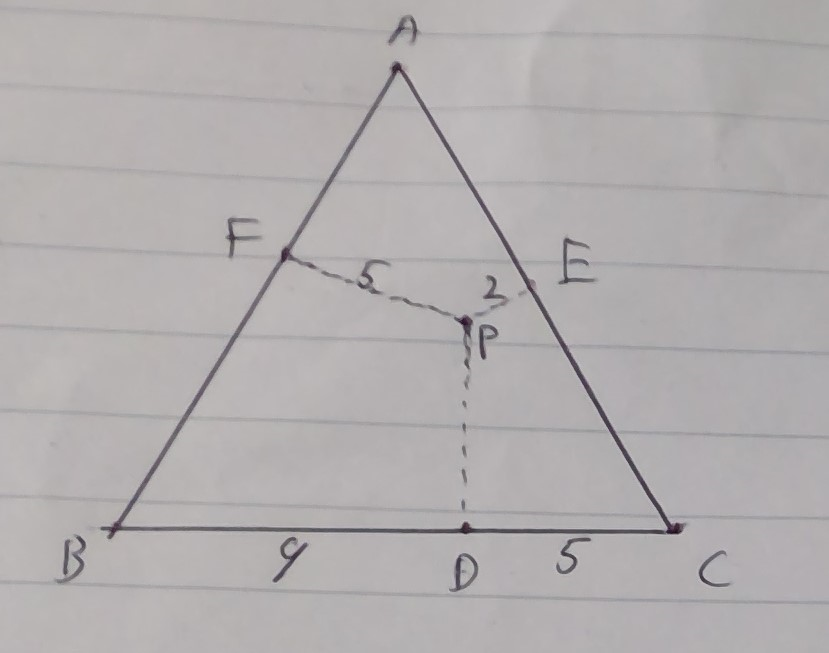
解説:まず、下の図のようにQ,R,Hを取ります。
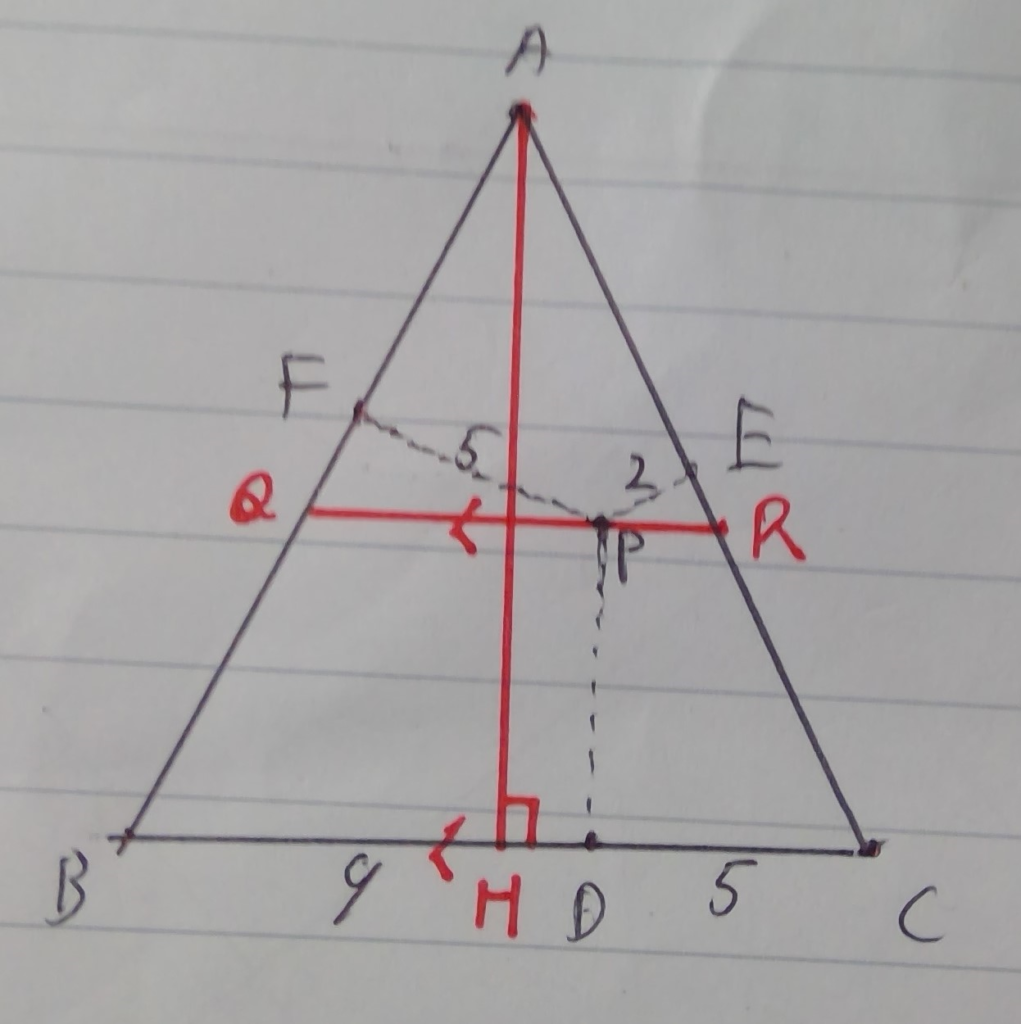
そして、下の図のようにまずわかる条件を埋めていきます。
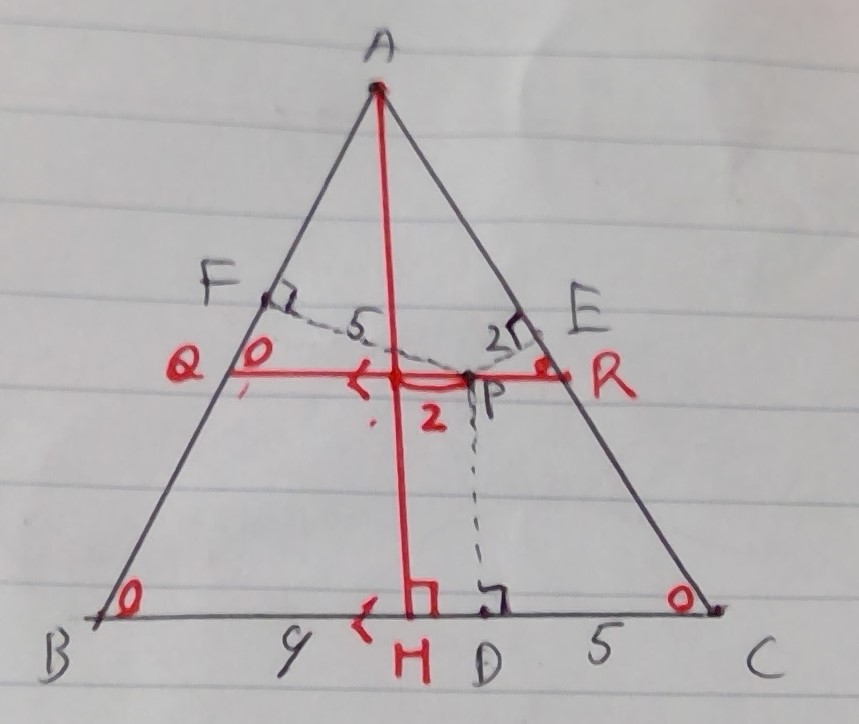
この時、上の図からもわかるように⊿FQP∽⊿ERPであるから、QP:PR=5:2です。
またPQ-PR=4であることは上の図から自明なので、PQ=20/3、三平方の定理を使うことでFQ=(5√7)/3が分かります。
また、⊿FQP∽⊿HBAより、FQ:PQ=BH:ABと分かるため、これに数値を代入することで、AB=4√7です。
これは二等辺三角形と直角を相似に持ち込むというところがポイントだったかなと思います。
問4:
問題:黒板に3つの相異なる正の整数が書かれている。黒板に実数a,b,cが書かれている時、それぞれを(b+c)/2,(c+a)/2,(a+b)/2に書き換えるという操作を行う。この操作を2021回行ったとき黒板に書かれた3つの数はすべて正の整数であった。この時、最初に黒板に書かれていた3つの正の整数の和としてありうる最小の値を求めよ。
解説:
| 最初に書かれた数 | a | b | c | それぞれの差(順不同) | b-a | c-b | c-a |
| 1回目の操作後に書かれた数 | (b+c)/2 | (a+c)/2 | (a+b)/2 | それぞれの差(順不同) | (b-a)/2 | (c-b)/2 | (c-a)/2 |
| 2回目の操作後に書かれた数 | (2a+b+c)/4 | (a+2b+c)/4 | (a+2b+c)/4 | それぞれの差(順不同) | (b-a)/4 | (c-b)/4 | (c-a)/4 |
上の表からもわかるように1回操作を施すごとに差が半分になっていきます。
また施した後の3つの数がすべて整数という条件から、最初に黒板に書かれた数の差は0以下ではない2^2021の倍数とわかります。
よって、最初に黒板に書かれた数が正の整数であるという条件から、最小のものを1、それぞれの差をいずれも2^2021とすることで、3つの組み合わせは(1,1+2^2021,1+2*2^2021)であり、求める3つの正の整数の和は3*2^2021+3であるとわかります。
これは差に注目するというポイントと正の整数という条件さえ押さえていればミスなく答えを書けると思います(^^♪
数学好き大歓迎‼ プログラミングするならTechAcademy‼
皆さん、「プログラミングで実用的なものを作ってみたい」とか、「Webやフリーランスで短期間で副業収入得たいな」とか思ったことはありませんか。
でも、素人がやろうとしても難しすぎて、挫折してしまうことが多いです。
そんな時にお勧めしたいのが、利用者数,満足度ともに業界No.1のプログラミングスクール、Techacademyです‼
TechAcademyなら…
- 他社とは比べ物にならない圧倒的コストパフォーマンス‼
- 現役エンジニアによる徹底サポートで初心者でも安心‼
- 副業として稼げるまでのサポート保証付き‼‼
- 期限がないから自分のペースでできる‼‼
さらに、TechAcademyでは20を超えるコース(初めての副業コース,Web開発,動画編集コース,ゲーム開発, エンジニア転職保証コース,スマホアプリ開発,Pythonコース,…)の中からあなたに合ったコースを自由に選択できます‼
数学オリンピックの問題を解けるようになるには
正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか本選の最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。
というわけで、数学オリンピック対策でぜひ読んでおくべき本を紹介したいと思います‼‼
下の記事から抜粋しました。もっと詳しく知りたい方は、ぜひ下の記事を読んでください‼
パーフェクトマスターシリーズ
これは、特定の分野をしっかり固めたい方にお勧めです。
大事な問題だけがセレクトされているので、その分野の問題をしっかり鍛えることができます。
初等整数を鍛えたい方にオススメ‼‼
これは、初等整数をマスターしたい方にお勧めです。
初等整数の問題はよく本選の大門1なんかで出題されることが多いので、そういった類の問題を解けるようになりたい方はこの本がおすすめです‼‼
平面幾何を鍛えたい方にオススメ‼‼
下の本は平面幾何を鍛えたい方にオススメの本です。
「数学オリンピックの幾何の問題を解いていると、「こんな発想が出てくるわけないだろ!!」みたいな問題にあたることはよくあると思います。
この本を読むことで、そういう問題たちをすらすら解けるようになります‼‼
代数・解析を鍛えたい方にオススメ‼‼
下の本は、代数、解析を鍛えたい方におススメの本です
数学オリンピックの問題の中でも、「絶対解けるか!!」みたいなレベルの問題って稀にあるじゃないですか。
こういう問題は、代数・解析の分野に入ることが多いです。
数学オリンピックで、難しい問題を解いてほかの受験生と差をつけたい方にはこの本をお勧めします‼
組み合わせ論を鍛えたい方にオススメ‼‼
下の本は、組み合わせ論を鍛えたい方におススメの本です。
数学オリンピックの場合の数の問題は、ほかの分野に比べてそこまで難しい問題が出題されることはあまりないんですが、とにかくめちゃくちゃミスしやすいように巧妙に仕組まれています。
そんなミスしやすいポイントをしっかり克服するためにも、ぜひこの本は見ていただきたいです。
過去問をひたすら解きまくる
これも結構おすすめです。過去問を全部解いていれば、実質数学オリンピックに関係する問題を全部網羅したようなものなので、完璧にマスターしたい方にはこちらの方法をお勧めします‼‼
ほかにも過去問についてはいろんな著者がいろんな本を出版しているので、ぜひそちらの本も調べてみてください。(下リンク)
数学オリンピックの参考書は高すぎる‼‼
今紹介させていただいた本を見て思ったかもしれませんが、とにかくこういった類の参考書は高いです。
でも、なんと「kindle Unlimited」なら、今紹介した本が月額980円払うだけでで読むことができます‼‼‼
1冊読むだけで余裕で元を取れますね。
さらに、今だけ初月無料なので、初月だけ契約すれば、本当に1銭も払わず、あの高額な本たちを読むことができます😎
私もこれを使っていて、「kindle Unlimited」なら、大体の本が無料で読めちゃうので、知りたいことがあったら簡単に本で調べたり、本で勉強したりすることができます。
また、息抜きに読書したいときにも役に立つので、ぜひこれは、お勧めしたいです‼‼
↓興味がある方はこちら‼‼
終わりに:
1番から4番に関しては例年に比べて易しかったと思います。
ただ、ミスしやすい場所が結構多かったのでその辺は気を付けましょう。
また続きの問題についての投稿もありますので、関連記事のところなどから、それもあわせてお読みおいただければ光栄です。



プロフィール
このブログの情報が少しでも役に立てれば嬉しいです。