初めに
今回は、数学オリンピック2019予選の問題の解答・解説をしていきたいと思います‼‼
ノーヒントで解いてみたいという方は、下のリンクをクリック‼‼
第29回(2019年)JMO予選の問題 (imojp.org)
また、この記事の最後に、「数学オリンピックの問題を解けるようになる方法」について解説していますので、興味がある方はそちらのほうも読んでいただければ光栄です。
注意
この記事では、日本数学オリンピック予選2019の問題のうち、問5から問8までしかしていません。
ほかの問題の解答・解説が気になる方は、下のリンクをクリック‼‼
それでは日本数学オリンピック予選2019の解答・解説を見ていきましょう‼‼
\“プログラミング”が数学力を金に変える‼/
↑必要なのは名前とメアドだけ,顔出し不要,完全オンライン完結‼
日本数学オリンピック予選2019 解答・解説 問5
問題:
97,100,103で割った余りが、それ添え32,33,34である正の整数のうち最小のものを求めよ。
解答・解説(解法①):
これは、めんどくさいですが素直に解きます。
もっと数が増えたり、ややこしくなったりしたら、中国剰余定理を使うのが一番早いんですが、今回は、数値が計算しやすいようにできているので、ごり押せば解けます。
問題の条件より、下のようにあらわすことができます。
97x+32=100y+33=103z+34
これより、下のことが導かれます。
- 97x-100y=1
- 100y-103z=1
- 97x-103z=2
さらに、上の不定方程式は、下のように解くことができます。(別にコンピューターを使わなくても、xとyとzの値は高々1,2程度しか変わらないので、それに注目して解くことができます。)
- x=33+100k,y=32+97k
- y=34+103m,z=33+100m
- x=34+103n,z=32+97n
これは、先ほど解いた方程式から、k,m,nの最小の値は、それぞれ、34,32,33であり、その時のx,y,zの値は、3433,3330,3233と分かります。
よって、もとめる答えは、
3433*97+32=3330*100+33=3233*103+34
より、333033と分かります。
解答・解説(解法②)
上のようにごり押しで解くこともできるんですが、この問題は、もっと楽に解くこともできるので、その解法を紹介したいと思います。
求める値をnとします。
この時、3n+1=3(n-32)+97=3(n-33)+100=3(n-34)+103
なので、3n+1は、97の倍数であり、100の倍数であり、103の倍数でもあることがわかります。
よって、nの最小値は、(97*100*103-1)/3より、n=333033と分かります。
また、333033を97で割ったときの余りは32であり、100で割ったときの余りは33であり、103で割ったときの余りは34なので、答えは、333033です。
日本数学オリンピック予選2019 解答・解説 問6
問題:
正120角形のいくつかの頂点に印がついている。印のついた3つの頂点の組であって、頂角18°の二等辺三角形の3頂点をなすようなものが存在しないとき、印のついた頂点の個数としてありうる最大の値を求めよ。
解答・解説:
まず、頂角が18°の三角形なのかまず考えていきます。
頂角が18°という条件から、円周角の定理より、下のことがわかります。
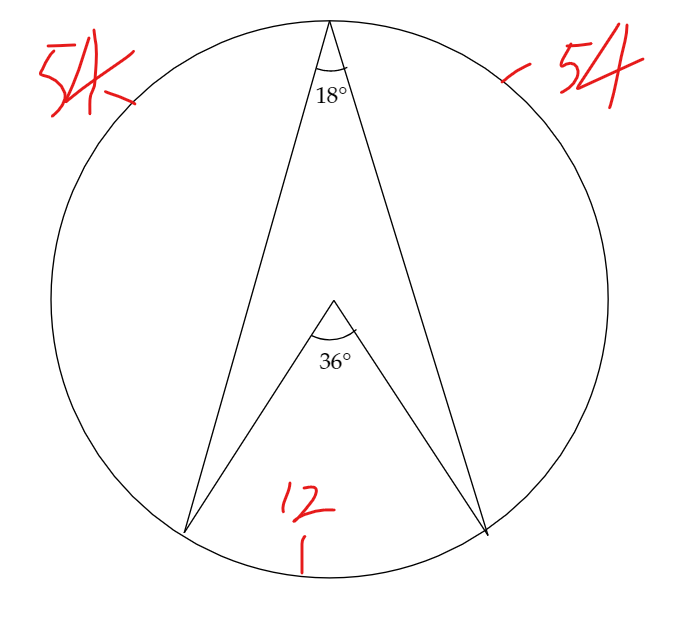
よって、12と54の最大公約数を取って、正120角形は正20角形が6つと考えることができます。
次は、視点を変えます。「印があるマスで問題の条件に合う三角形を作ることができない」ようにすることと、「印がないマスが三角形を作れないようにしている」ことは同じなので、
次は、視点を変えます。印がない頂点に注目すると、下のように、一つ印がない頂点があるだけで、最大3個の問題の条件に合う三角形を作れないようにすることができます。
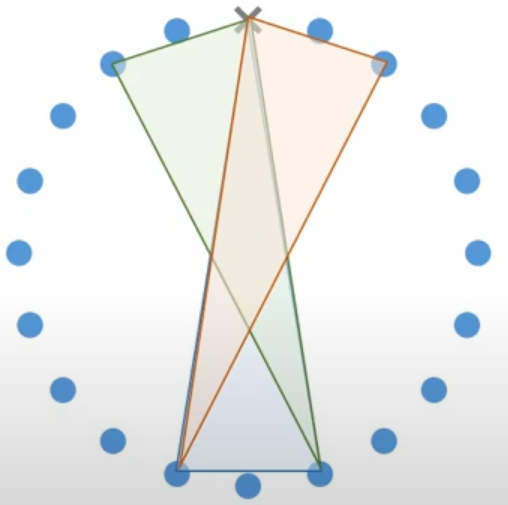
よって、印をつけることができる頂点の数は、20-20÷3個以下、つまり、13個以下であることがわかります。
また、下のようにすれば、13個でも成立します。
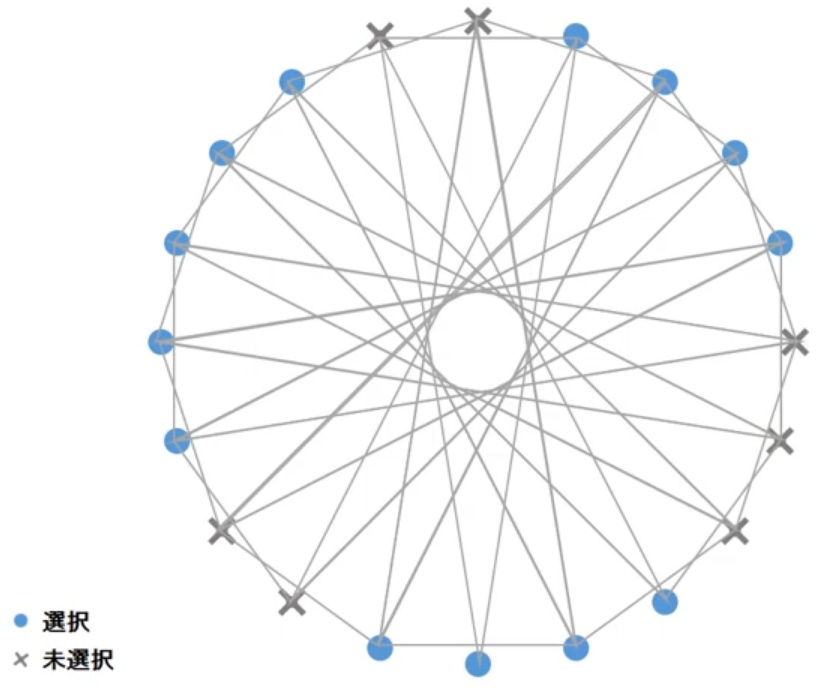
よって、もとめる答えは、13×6より、78個と分かります。
この問題は6番とは思わないくらい難しかったと思います。
日本数学オリンピック予選2019 解答・解説 問7
問題:
整数係数2次多項式P,Q,Rは以下の条件を満たすとする。このときR(x)として考えられるものを全て求めよ。
- P(1)=P(2)=Q(3)=0
- 任意の実数xに対して、P(x)2+Q(x)2=R(x)2
- P,Q,Rのすべての係数を割り切る2以上の整数はない。
- P,Qの2次の係数は0でなく、Rの2次の係数は正である。
解答・解説:
P(1)=P(2)=0より、P(x)は、0以外の整数aを用いて、
P(x)=a(x-1)(x-2)
とあらわすことができます。
なので、
P(x)2=R(x)2 -Q(x)2=(R(x)+Q(x))(R(x)-Q(x))=a(x-1)2(x-2)2
ということに注目します。
この時、以下のように3つのパターンに分けて考えることができます。
R(x)+Q(x)=b(x-1)(x-2),R(x)-Q(x)=c(x-1)(x-2)のとき
この時、
Q(x)=((b-c)/2)×(x-1)(x-2)
なので、Q(x)=3より、Q(x)の2次の係数が0になってしまうため、不適。
R(x)+Q(x)=b(x-1)2,R(x)-Q(x)=c(x-2)2のとき
これは、Q(x)を、-Q(x)にすると、下のパターンとやってることが同じになります。
R(x)+Q(x)=b(x-2)2,R(x)-Q(x)=c(x-1)2のとき
このとき、
Q(x)=(b/2)(x-2)2 – (c/2)(x-1)2
なので、Q(3)=0より、b=4cと分かります。
これを代入すると、
- P(x)=±2c(x-1)(x-2)
- Q(x)=2c(x-2)2 – (c/2)(x-1)2
- R(x)=2c(x-2)2 – (c/2)(x-1)2
となります。
ここで、P,Q,Rのすべての係数が整数であることと、Rの二次の係数が正であることから、cは2以上の2の倍数と分かります。
しかし、もし、cが4以上の2の倍数だとすると、P,Q,Rのすべての係数を割り切る数(2で割り切れてしまいます。)が存在してしまうため、cは2しかありえません。
よって、もとめるRの多項式の値として考えられるものは、
R(x)=5x2-18x+17
のみだとわかります。
日本数学オリンピック予選2019 解答・解説 問8
問題:
AB>ACを満たす三角形ABCの内心をIとし、辺AB,ACを1:8に内分する点をそれぞれD,Eとする。三角形DIEが一辺の長さが1の正三角形であるとき、線分ABの長さを求めよ。ただし、XYで線分XYの長さを表すものとする。
解答・解説:
これは、図を描くところに気を使う必要があります。
もし、下のように図を描いたとします。
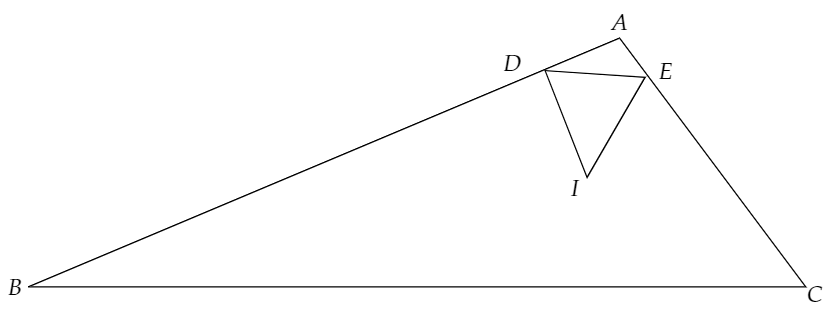
この時、点Iから、AB,ACに垂線を引き、垂線の足をそれぞれ、P,Qとすると、下のようになります。
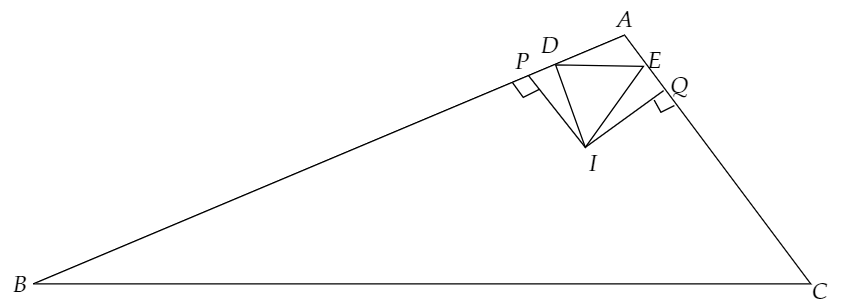
しかし、この時、⊿PID≡⊿QIEより、AP=AQ,DP=EQとなるため、AD=AEとなります。
これは、AB>ACに反しています。
よって、図は下のように書くべきだということがわかります。
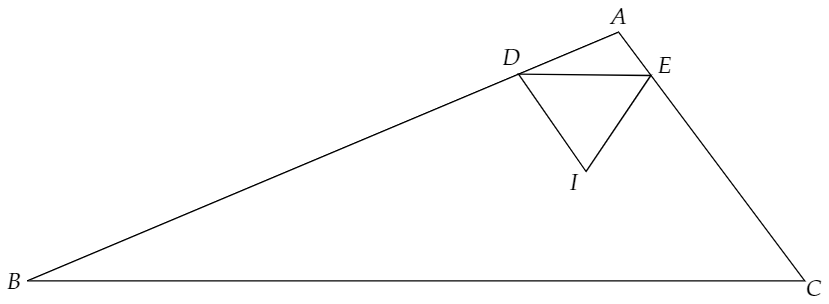
そして、先ほどと同様に点Iから辺AB,ACに下した垂線の足をP,Qとします。
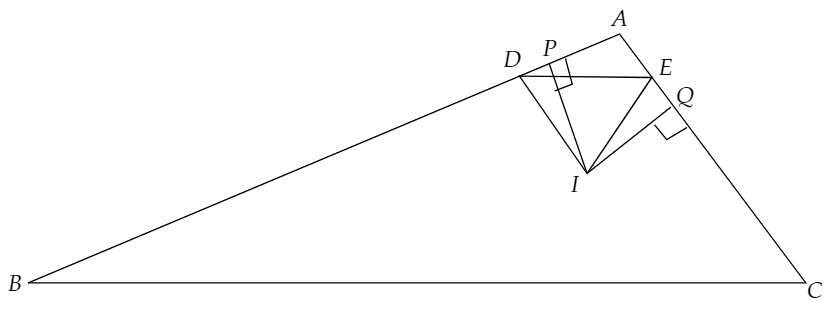
この時、四角形APIQに注目すると、∠BAC=120度となります。
次に、DE//BCと、角度の条件60度を生かすために、下のようにEIとBCの交点Rを取ります。
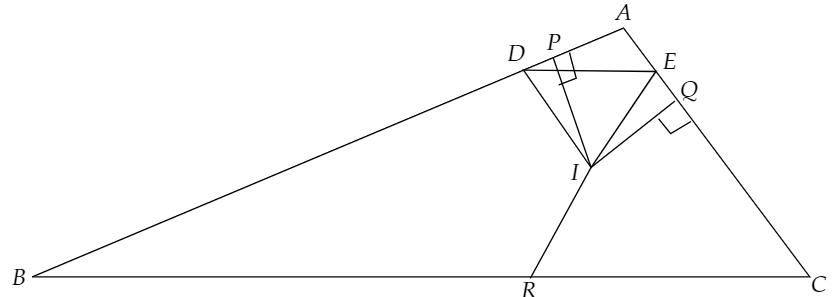
このとき、2角1辺相等より、⊿AIC≡RICとなります。
よって、⊿ECRに注目すると、核の二等分線の定理より、EI:IR=EI:AI=8:9と分かります。
なので、AIの長さは9/8と分かります。
さあに、⊿AIDに注目すると、∠DAI=60°,DI=1,AI=9/8より、余弦定理から、ADの長さは、
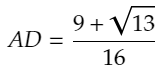
と分かるため、もとめるABの長さは、
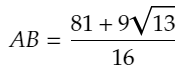
と分かります。
数学オリンピックの問題を解けるようになるには
正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか本選の最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。
というわけで、数学オリンピック対策でぜひ読んでおくべき本を紹介したいと思います‼‼
パーフェクトマスターシリーズ
これは、特定の分野をしっかり固めたい方にお勧めです。
大事な問題だけがセレクトされているので、その分野の問題をしっかり鍛えることができます。
初等整数を鍛えたい方にオススメ‼‼
これは、初等整数をマスターしたい方にお勧めです。
初等整数の問題はよく本選の大門1なんかで出題されることが多いので、そういった類の問題を解けるようになりたい方はこの本がおすすめです‼‼
平面幾何を鍛えたい方にオススメ‼‼
下の本は平面幾何を鍛えたい方にオススメの本です。
「数学オリンピックの幾何の問題を解いていると、「こんな発想が出てくるわけないだろ!!」みたいな問題にあたることはよくあると思います。
この本を読むことで、そういう問題たちをすらすら解けるようになります‼‼
代数・解析を鍛えたい方にオススメ‼‼
下の本は、代数、解析を鍛えたい方におススメの本です
数学オリンピックの問題の中でも、「絶対解けるか!!」みたいなレベルの問題って稀にあるじゃないですか。
こういう問題は、代数・解析の分野に入ることが多いです。
数学オリンピックで、難しい問題を解いてほかの受験生と差をつけたい方にはこの本をお勧めします‼
組み合わせ論を鍛えたい方にオススメ‼‼
下の本は、組み合わせ論を鍛えたい方におススメの本です。
数学オリンピックの場合の数の問題は、ほかの分野に比べてそこまで難しい問題が出題されることはあまりないんですが、とにかくめちゃくちゃミスしやすいように巧妙に仕組まれています。
そんなミスしやすいポイントをしっかり克服するためにも、ぜひこの本は見ていただきたいです。
過去問をひたすら解きまくる
これも結構おすすめです。過去問を全部解いていれば、実質数学オリンピックに関係する問題を全部網羅したようなものなので、完璧にマスターしたい方にはこちらの方法をお勧めします‼‼
ほかにも過去問についてはいろんな著者がいろんな本を出版しているので、ぜひそちらの本も調べてみてください。(下リンク)
数学オリンピックの参考書は高すぎる‼‼
今紹介させていただいた本を見て思ったかもしれませんが、とにかくこういった類の参考書は高いです。
でも、なんと「kindle Unlimited」なら、今紹介した本が月額980円払うだけでで読むことができます‼‼‼
1冊読むだけで余裕で元を取れますね。
さらに、今だけ初月無料なので、初月だけ契約すれば、本当に1銭も払わず、あの高額な本たちを読むことができます😎
私もこれを使っていて、「kindle Unlimited」なら、大体の本が無料で読めちゃうので、知りたいことがあったら簡単に本で調べたり、本で勉強したりすることができます。
また、息抜きに読書したいときにも役に立つので、ぜひこれは、お勧めしたいです‼‼
↓興味がある方はこちら‼‼
終わりに
いかがでしたか。
ほかにも数学オリンピックの解説している記事もありますので、そちらのほうも見ていただければ光栄です‼‼
それでは次の記事で‼


プロフィール
このブログの情報が少しでも役に立てれば嬉しいです。