初めに
皆さんは、下の問題を解けますか。
15の倍数でなく、18の倍数でもなく、35の倍数でもないような630以下の数の個数を求めよ。
まあ、問題自体は解くのは簡単なんで、皆さんも解くことができると思います。
この記事を読んだら、この問題を5秒で解けます。
それでは、トーシェント関数についてみていきましょう‼
オイラー関数(トーシェント関数)とは?
オイラーのφ関数(トーシェント関数)とは、自然数nに対して、n以下のnと互いに素でない数の個数を表す関数で、φ(n)と表記します。
例えば、
- φ(1)=0
- φ(7)=6
- φ(9)=7
となります。
トーシェント関数に関する美しい性質
つぎは、トーシェント関数に関するシンプルで美しい性質を2つ紹介していきたいと思います‼
1つ目
一つ目は、オイラーの定理と呼ばれているやつです。
この定理は、「フェルマーの小定理を拡張したもの」と呼ばれるくらい強力なものです。
どういうものかというと、
nが正の整数でaをnと互いに素な正の整数としたとき,

が成立する。(aの乗数のところはn以下のnと互いに素な自然数の数)
というものです。
これの証明や、これを利用した練習問題については下の記事をどうぞ‼‼
上の記事を読んでわかったと思いますが、この定理を使えば、
7400の下3桁をもとめよ。
【必見!!】オイラーの定理(数論,合同式,mod)とその証明 練習問題付き‼
といった問題も簡単に解くことができます‼
2つ目
これは、知っていたらかなり便利なやつです。
この記事の一番最初に紹介した問題もこの性質を利用して解くことができます。
どういう性質かというと、
nの素因数分解が、
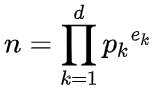
のように与えられているとき、
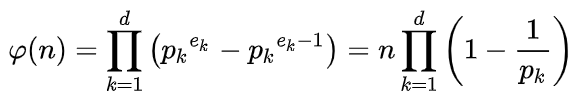
というものです。(dはnの素因数の個数)
これだけも見せられてもなにがなんだかわからない方もいると思いますので、具体例を見ていきましょう‼
例えば、
105と互いに素な自然数の数を求めよ。
といった問題があったとします。
本来なら、この問題は、便宜図を描いてごちゃごちゃしないといけないのが、先ほどの性質を使うことで、
φ(105)=105×(1-1/3)×(1-1/5)×(1-1/7)=48
と分かるため、先ほどの問題の答えは、48と一瞬でわかります。
つぎは、この性質の証明を紹介しようとおもいます‼
この性質の証明
これは、そこまで難しくありません。
ただ、これを証明するためには、二つの補題を証明しないといけないので、まずはそっちから片付けていきます。
補題1
pを素数とするとき、
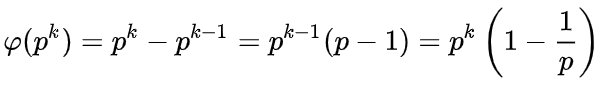
が成り立つ。
補題1の証明
実質、
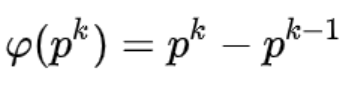
を証明するだけです。
これの証明は簡単で、pと互いに素でないものの個数は、pが素数であることから、pk以下の整数の中で、 pk/p=pk-1個であることがわかります。
よって、 先ほどの式が導かれることがわかります。
補題2
nとmを互いに素な自然巣とする。
この時、
φ(mn)=φ(m)φ(n)
が成り立つ。
補題2の証明
これは、乗法性ともいわれます。
イメージしやすいように、mnを下のようにあらわします。
| 1 | 2 | … | m-1 | m |
| m+1 | m+2 | … | 2m-1 | 2m |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| m(n-2)+1 | m(n-2)+2 | … | m(n-1)-1 | m(n-1) |
| m(n-1)+1 | m(n-1)+2 | … | mn-1 | mn |
この中で、mnと互いに素である必要十分条件を考えます。
まず、行に注目します。
この時、~m+rとなっているもののうち、rとmが互いに素でないとき、2以上のrとmの最大公約数dを取ることができ、mnとその数は、ともにdで割り切れてしまうため、rがmと互いに素である場合の時しか、mnと互いに素である数がその列に含まれていないことがわかります。
よって、rがmと互いに素である列を考えればいいことがわかります。(φ(m)個)
次に、列に注目します。
列が同じすべての数は、nで割った余りがすべて異なります。
よって、先ほどと同様の理屈で、それぞれの列に対して、nと互いに素である行は同じ数だけ存在します。(φ(n)個)
また、mとnのどちらとも互いに素である数は、mnと互いに素なので、
mとnが互いに素であるとき、
φ(mn)=φ(m)φ(n)
がなりたちます。
これで、補題2の証明は完了です。
証明の続き
続きといっても、下のままです。
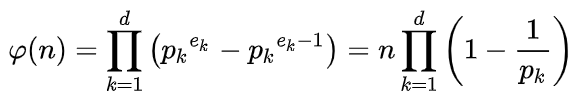
上の記号はk=1からdまでの積を表すものとします。
終わりに
いかがでしたか。
これを使えば、二項定理でごり押していた計算をサラッと解けるようになったり、便宜図を描いてごちゃごちゃしていた問題を一瞬で解いたりすることができます。
ほかにも面白い記事がたくさんありますので、そちらの方も見ていただければ光栄です。
それでは次の記事で‼‼



プロフィール
このブログの情報が少しでも役に立てれば嬉しいです。