初めに
この記事は下のリンクの記事の補足内容となっております。基礎からしっかり学びたい方や、基本をもう一度復習したい方はぜひ下の記事を読んでからみてください。
また、このサイトは下の本を参考にしています。よかったら買ってみてください。
 | 高等学校 数学B 高校用 文部科学省検定済教科書 [数B331] 第一学習社 価格:2,200円 |
それでは公式と証明を見ていきましょう‼‼
独立である確率に関する基本公式
独立である確率変数X,Yに対して下の式が成り立ちます。
E(XY)=E(X)E(Y)
V(X+Y)=V(X)+V(Y)
この公式を証明していきます。
講師は全員京大生だから安心独立である事象に対する基本公式の証明
同時分布が
| 縦:X,横:Y | y1 | y2 | … | ym | 計 |
| x1 | p11 | p12 | … | p1m | p1 |
| x2 | p21 | p22 | … | p2m | p2 |
| … | … | … | … | … | … |
| xn | pn1 | pn2 | … | pnm | pn |
| 計 | q1 | q2 | … | qm | 1 |
である二つの確率変数X,Yについて考えます。
【読むだけで全部マスターできる‼‼】数Bの確率・統計分野で説明したとおり、独立である二つ確率変数と、確率p,qに対して、pkl=pk×qlが成り立ちます。なので、確率変数XYに対する期待値E(XY)について下のように変形することができます。
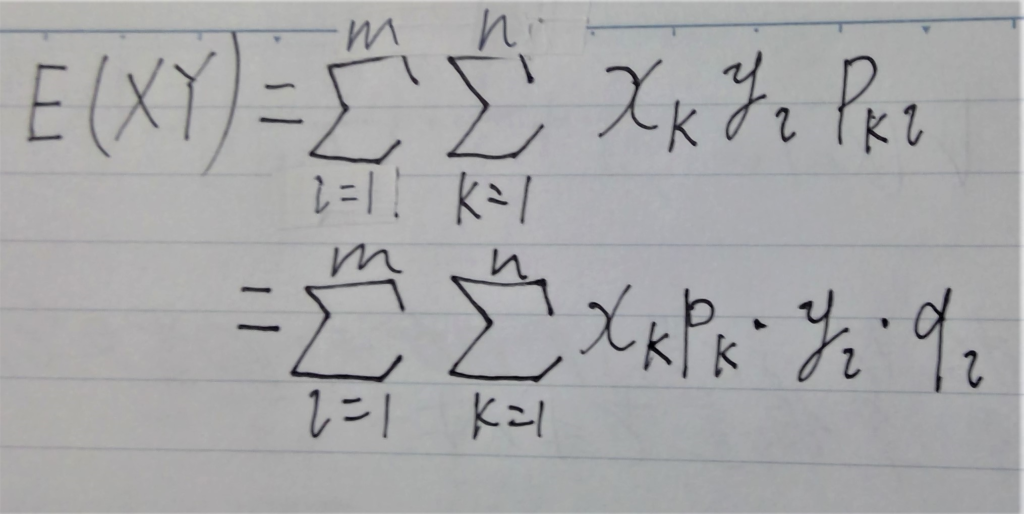
また、これを、下のように変形させたとしても、上の値と、1対1に対応させることができるため、下のように変形することができます。(展開するとどうなるかを考えてもらうと、わかると思います。ちなみに項の和もちゃんとどちらもklになっています。)
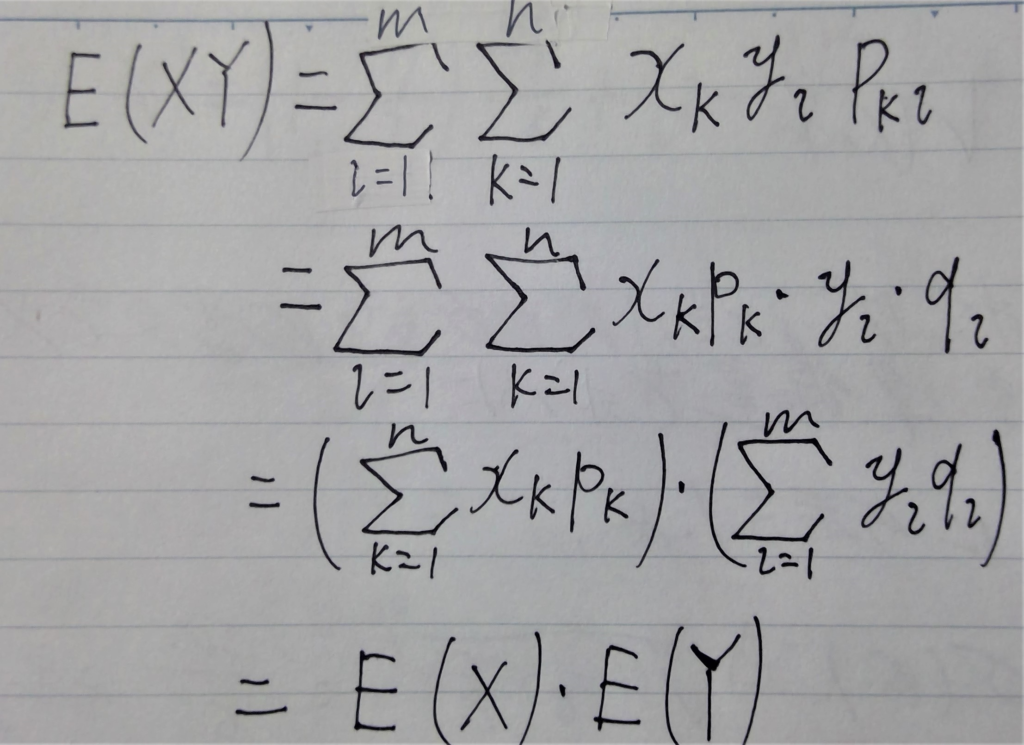
これでXYの期待値に関する公式を導き出せました。
次に、分散の和についての公式を導き出します。
これは下の写真の通りです。変形でわからないところがある方は、下のリンクをクリックして読んでください。
※E(X+Y)=E(X)+E(Y)は自明です。もし理解できないという方は、もう一度定義から理解し直したほうがいいでしょう。→【読むだけで全部マスターできる‼‼】数Bの確率・統計分野
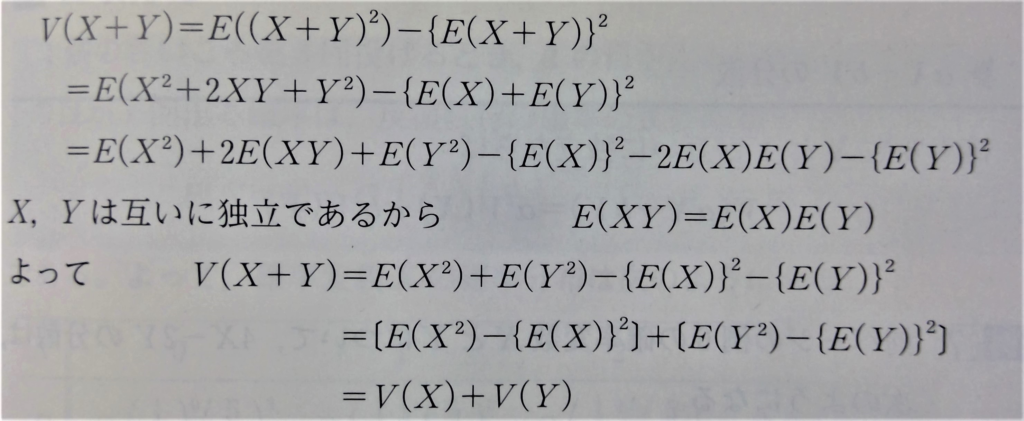
これで、分散の和についての公式を導き出せました。
これで証明完了です。
終わりに
確率分布・確率変数の範囲以外の確率・統計分野についてもっと知りたい方は、ぜひ、下のリンクの記事を読んでください。
ほかにも面白い記事がたくさんありますので、そちらのほうも見ていただければ光栄です。
それでは次の記事で‼‼




プロフィール
このブログの情報が少しでも役に立てれば嬉しいです。