初めに
数B の確率分布の分野を一気に解説していきます。この記事を読むだけで、数B の確率の分野が全部理解できます。
インターネットを活用した次世代型完全個別指導塾【ネット松陰塾】なお、このサイトの引用元は下の本です。
 | 高等学校 数学B 高校用 文部科学省検定済教科書 [数B331] 第一学習社 価格:2,200円 |
確率変数と確率分布
まず、確率変数と確率分布について解説します。
さいころを例に見ていきましょう。
| 確率変数X | 1 | 2 | 3 | 4 | 5 | 6 |
| 確率P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
サイコロの目でいうところの「1,2,3,4,5,6」のように、どの値を取るかが試行の結果によって定まり、その取りうる値の各々に対してその値を取る確率が定まるような変数を確率変数といい、Xと表します。
また、確率変数のとりうる値が、x1、x2、…xnの時、Xが一つの値を取る確率P(X=xk)と表します。
サイコロを例に出すと、P(X=1)=1/6になります。
また、これを一般化して、下の表のように、XとPの関係を表したものを、Xの確率分布または、単に分布といい、Xはこの分布に従うといいます。
| X | x1 | x2 | …. | xn |
| P | p1 | p2 | …. | pn |
練習問題を解いてみたいという方はこちらから↓
【受験生必見‼‼】数Bの確率・統計分野(練習問題 確率変数と確率分布編)
期待値・分散・標準偏差
次は、期待値・分散・標準偏差について解説していきます。
Xが下の確率分布に従うとします。
| X | x1 | x2 | …. | xn |
| P | p1 | p2 | …. | pn |
この時、
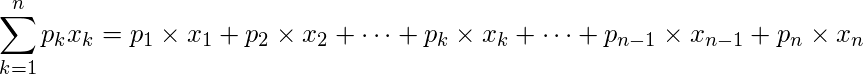
を、期待値といい、E(X)または、mと表します。
サイコロを例に出すと、

と計算することで、サイコロの期待値が3.5であることを導き出せます。
分散V(X)を下のように定義します。(mは先ほど定義した期待値です。)
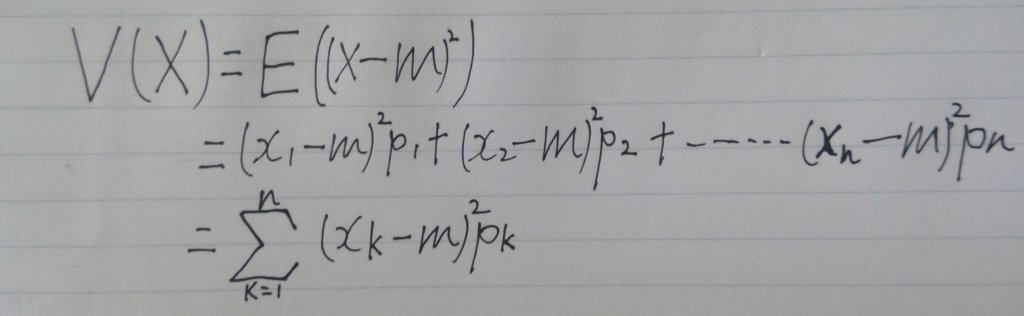
さらに、標準偏差σ(X)を下のように定義します。
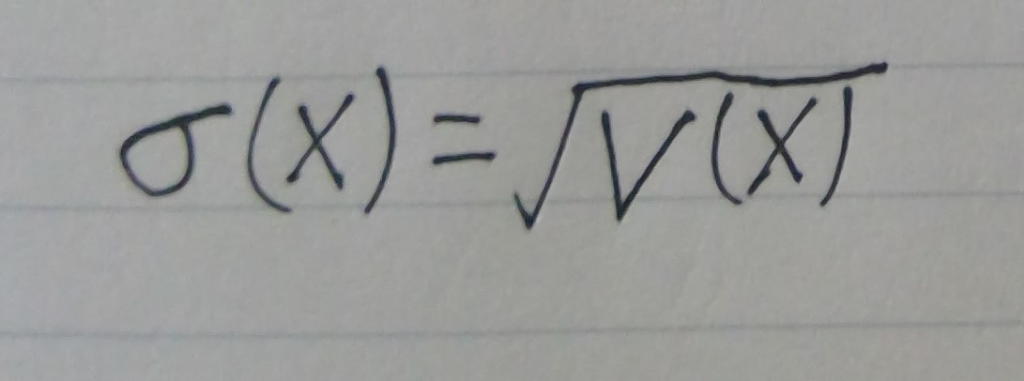
こんなものだけ見せられてもわからないと思うので、サイコロを例にして説明していきます。
サイコロの場合、期待値は先ほど求めたので、(3.5)分散および標準偏差は、下のように計算することができます。
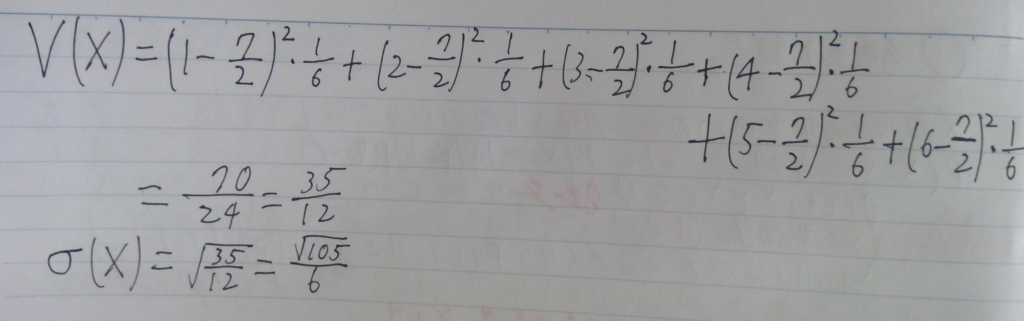
また、分散については下の公式が成り立ちます。(標準偏差はこれに「√」をつければいいだけです。)
分散:V(X)=E(X²)-{E(X)}²
つまり、
Xの分散=(X²の期待値)-(Xの期待値)²
が成り立ちます。
これの証明については下のリンクをクリックして是非読んでください。
期待値・分散・標準偏差の練習問題を解いてみたいという方は下のリンクをクリックしてください。
【受験生必見‼‼】数Bの確率・統計分野(練習問題 期待値、分散、標準偏差編)
次は確率変数の変換という話をします。
 | 高等学校 数学B 高校用 文部科学省検定済教科書 [数B331] 第一学習社 価格:2,200円 |
確率変数の変換
確率変数Xと、定数a,bに対して、Y=aX+bとすると、Yも確率変数となり、下の定理が成り立ちます。
E(Y)=aE(X)+b
V(Y)=a²V(X)
σ(Y)=|a|σ(X)
これの証明については下のリンクをクリックして読んでください。
サイコロの場合を例に出すと、y=2x+1とすると、確率分布
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
が、
| Y | 3 | 5 | 7 | 9 | 11 | 13 |
| P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
となります。
これの練習問題を解いてみたいという方はこちら↓
【受験生必見‼‼】数Bの確率・統計分野(練習問題 確率変数の変換編)
同時分布と独立
今まで、確率変数は一つだけでしたが、当然確率変数が2つや3つの場合だってあります。その時の確率分布を同時分布といい、下の表のように表されます。
| 縦:X,横:Y | y1 | y2 | … | ym | 計 |
| x1 | p11 | p12 | … | p1m | p1 |
| x2 | p21 | p22 | … | p2m | p2 |
| … | … | … | … | … | … |
| xn | pn1 | pn2 | … | pnm | pn |
| 計 | q1 | q2 | … | qm | 1 |
また、上の分布表において、pkl=pk×ql となるとき、二つの確率変数X,Yは、独立であるといい、独立でない場合の時を、従属であるといいます。
例を出すと、大小違うサイコロを振って、大が2で、小が3となる確率は、1/36であり、大が2である確率(1/6)×小が3である確率(1/6)=1/36となるため、この二つは、「独立である」といえます。
もし、大小違うサイコロではなく、区別のないサイコロの場合、計算してもらえればわかりますが、独立ではなく、「従属である」といえます。
また、互いに独立である事象X,Yに対して、下のことが成り立ちます。
E(XY)=E(X)E(Y)
V(X+Y)=V(X)+V(Y)
上の公式の証明については下のリンクをクリックして読んでみてください。
練習問題については下のリンクをクリックして解いてみてください。
【受験生必見‼】数Bの確率・統計分野(練習問題 同時分布と独立編)
また、期待値と分散の和と積について下の公式が成立します。
E(X)+E(Y)=E(X+Y)
E(X)×E(Y)=E(XY) (X,Yが互いに独立の時のみ成立)
V(X)+V(Y)=V(XY) (X,Yが互いに独立の時のみ成立)
V(X)×V(Y)=V(XY) (成立しない。←成立する場合もありますが、一般には成立しないという意味で書いています。)
二項分布
事象Aが起こる確率をpとし、この操作をn回繰り返すとする。この時、Aがr回起こる確率は、

であり、このような反復施行に対して、Aの起こる回数をXと置くと、確率変数Xの確率分布は下のようになります。
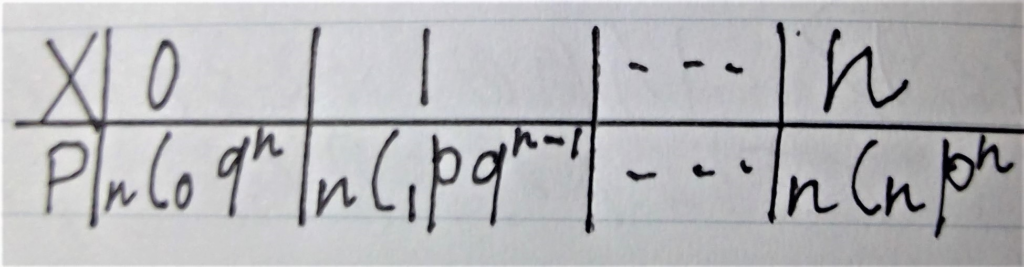
この確率分布を、二項分布といい、B(n,p)と表します。また、この時、Xは、「二項分布B(n,p)に従う」といいます。
さらに、Xが、二項分布B(n,p)に従うとき、q=1-pと置くと、下の公式が成り立ちます。
E(X)=np
V(X)=npq
σ(X)=√npq
上の公式の証明については、下のリンクをクリックして読んでください。
また、練習問題を解いてみたいという方は下のリンクをクリック‼‼
正規分布
この数Bの確率・統計の中の山場といえる正規分布という話をしていきたいと思います。
まず、一般に今までのように確率変数Xが「断片的な値をとる」とき、確率変数Xを、離散型確率変数といい、「連続的な値をとる」とき、確率変数Xを、連続型確立関数といいます。
また、確率変数Xが、連続型確率変数であるとき、縦軸をP、横軸をXとして、凸のグラフとしてあらわしたときに、下の図のように出てくる曲線を、分布曲線といいます。
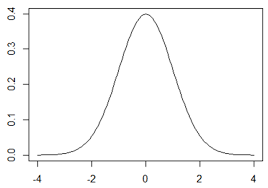
また、このとき、分布曲線をf(x)とすると、このf(x)のことを、確率密度関数といいます。(今までで言うところの、Pと同じような扱いだと思ってください。)
想像してもらえればわかりますが、連続型確率変数の期待値と分散は下のように定められます。(今までのPが、f(x)に、Σが、∫に変わっただけだと思っていただければ大丈夫です。)
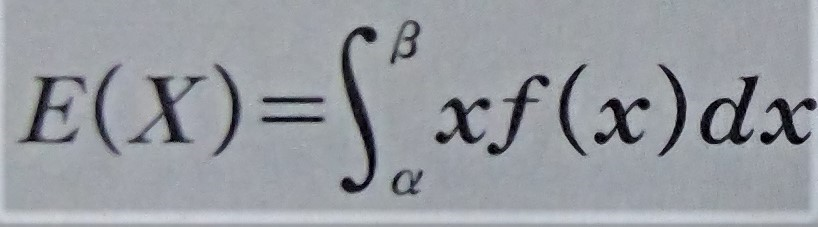
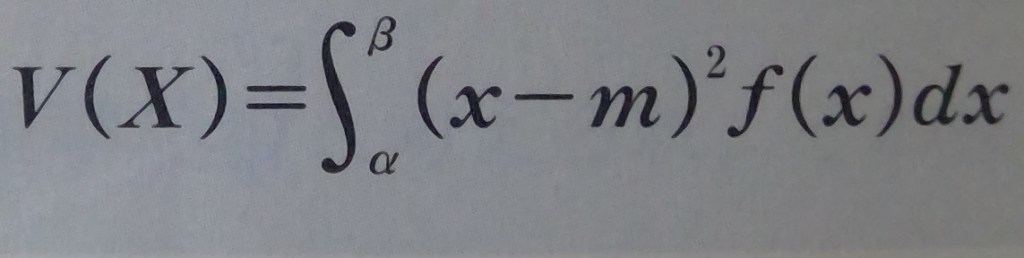
※ここで登場するmは、期待値のことを表しています。
そして、連続型確率変数の代表的なものとして、正規分布というものが挙げられます。この分布曲線は、正規分布曲線と呼ばれ、
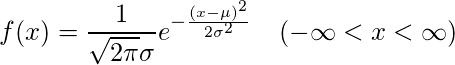
で表されます。
また、このとき、確率変数Xは、「正規分布N(m,σ²)に従う」といいます。
※上の式で登場するeですが、これはネイピア数と呼ばれ、値の大きさは大体、2.72です。
さらに、確率変数Xが、正規分布N(m,σ²)に従うとき、下の公式が成り立ちます。
E(X)=m
σ(X)=σ
上の公式の証明については下のリンクをクリックして読んでください。(結構難しいので、興味がある方だけで結構です。)
【超簡単!!】正規分布の期待値と標準偏差に関する公式とその証明
また、確率変数Xが、正規分布N(0,1)に従うとき、この時の正規分布を標準正規分布といいます。また、この分布は、下の図のように、y軸を中心として左右対称になっており、グラフの面積は1になります。(これの証明については下のリンクをクリック‼)
【超簡単!!】標準正規分布のグラフの面積に関する公式とその証明
さらに、確率変数Xが、正規分布N(m,σ²)に従うとき、Z=(X-m)/σと置くと、確率変数Zは、標準正規分布N(0,1)に従います。このことを正規分布の標準化とも言います。

上の正規分布の標準化に関する証明については下のリンクをクリックして読んでください。
次に、正規分布表の話をします。標準正規分布N(0,1)において、0からaまでの面積を表した表を、正規分布表といい、下のように表されます。
| Z | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | .0000 | .0040 | .0080 | .0120 | .0160 | .0199 | .0239 | .0279 | .0319 | .0359 |
| 0.1 | .0398 | .0438 | .0478 | .0517 | .0557 | .0596 | .0636 | .0675 | .0714 | .0753 |
| 0.2 | .0793 | .0832 | .0871 | .0910 | .0948 | .0987 | .1026 | .1064 | .1103 | .1141 |
| 0.3 | .1179 | .1217 | .1255 | .1293 | .1331 | .1368 | .1406 | .1443 | .1480 | .1517 |
| 0.4 | .1554 | .1591 | .1628 | .1664 | .1700 | .1736 | .1772 | .1808 | .1844 | .1879 |
| 0.5 | .1915 | .1950 | .1985 | .2019 | .2054 | .2088 | .2123 | .2157 | .2190 | .2224 |
| 0.6 | .2257 | .2291 | .2324 | .2357 | .2389 | .2422 | .2454 | .2486 | .2517 | .2549 |
| 0.7 | .2580 | .2611 | .2642 | .2673 | .2704 | .2734 | .2764 | .2794 | .2823 | .2852 |
| 0.8 | .2881 | .2910 | .2939 | .2967 | .2995 | .3023 | .3051 | .3078 | .3106 | .3133 |
| 0.9 | .3159 | .3186 | .3212 | .3238 | .3264 | .3289 | .3315 | .3340 | .3365 | .3389 |
| 1.0 | .3413 | .3438 | .3461 | .3485 | .3508 | .3531 | .3554 | .3577 | .3599 | .3621 |
| 1.1 | .3643 | .3665 | .3686 | .3708 | .3729 | .3749 | .3770 | .3790 | .3810 | .3830 |
| 1.2 | .3849 | .3869 | .3888 | .3907 | .3925 | .3944 | .3962 | .3980 | .3997 | .4015 |
| 1.3 | .4032 | .4049 | .4066 | .4082 | .4099 | .4115 | .4131 | .4147 | .4162 | .4177 |
| 1.4 | .4192 | .4207 | .4222 | .4236 | .4251 | .4265 | .4279 | .4292 | .4306 | .4319 |
| 1.5 | .4332 | .4345 | .4357 | .4370 | .4382 | .4394 | .4406 | .4418 | .4429 | .4441 |
| 1.6 | .4452 | .4463 | .4474 | .4484 | .4495 | .4505 | .4515 | .4525 | .4535 | .4545 |
| 1.7 | .4554 | .4564 | .4573 | .4582 | .4591 | .4599 | .4608 | .4616 | .4625 | .4633 |
| 1.8 | .4641 | .4649 | .4656 | .4664 | .4671 | .4678 | .4686 | .4693 | .4699 | .4706 |
| 1.9 | .4713 | .4719 | .4726 | .4732 | .4738 | .4744 | .4750 | .4756 | .4761 | .4767 |
| 2.0 | .4772 | .4778 | .4783 | .4788 | .4793 | .4798 | .4803 | .4808 | .4812 | .4817 |
| 2.1 | .4821 | .4826 | .4830 | .4834 | .4838 | .4842 | .4846 | .4850 | .4854 | .4857 |
| 2.2 | .4861 | .4864 | .4868 | .4871 | .4875 | .4878 | .4881 | .4884 | .4887 | .4890 |
| 2.3 | .4893 | .4896 | .4898 | .4901 | .4904 | .4906 | .4909 | .4911 | .4913 | .4916 |
| 2.4 | .4918 | .4920 | .4922 | .4925 | .4927 | .4929 | .4931 | .4932 | .4934 | .4936 |
| 2.5 | .4938 | .4940 | .4941 | .4943 | .4945 | .4946 | .4948 | .4949 | .4951 | .4952 |
| 2.6 | .4953 | .4955 | .4956 | .4957 | .4959 | .4960 | .4961 | .4962 | .4963 | .4964 |
| 2.7 | .4965 | .4966 | .4967 | .4968 | .4969 | .4970 | .4971 | .4972 | .4973 | .4974 |
| 2.8 | .4974 | .4975 | .4976 | .4977 | .4977 | .4978 | .4979 | .4979 | .4980 | .4981 |
| 2.9 | .4981 | .4982 | .4982 | .4983 | .4984 | .4984 | .4985 | .4985 | .4986 | .4986 |
| 3.0 | .4987 | .4987 | .4987 | .4988 | .4988 | .4989 | .4989 | .4989 | .4990 | .4990 |
| 3.1 | .4990 | .4991 | .4991 | .4991 | .4992 | .4992 | .4992 | .4992 | .4993 | .4993 |
| 3.2 | .4993 | .4993 | .4994 | .4994 | .4994 | .4994 | .4994 | .4995 | .4995 | .4995 |
| 3.3 | .4995 | .4995 | .4995 | .4996 | .4996 | .4996 | .4996 | .4996 | .4996 | .4997 |
| 3.4 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4998 |
| 3.5 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 |
| 3.6 | .4998 | .4998 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 |
| 3.7 | .4999 | .4999 | .4999 | .4999 | .49991 | .49992 | .49992 | .49992 | .49992 | .49992 |
| 3.8 | .49993 | .49993 | .49993 | .49994 | .49994 | .49994 | .49994 | .49995 | .49995 | .49995 |
| 3.9 | .49995 | .49995 | .49996 | .49996 | .49996 | .49996 | .49996 | .49996 | .49997 | .49997 |
| 4.0 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 |
| 4.1 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 |
| 4.2 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.3 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.4 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.5 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 | .49997 |
| 4.6 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 | .49998 |
| 4.7 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.8 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 | .49999 |
| 4.9 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 | .499995 |
| 5.0 | .499997 |
↑引用元:標準正規分布表
練習問題を解いてみたいという方は下のリンクをクリックして解いてみてください。
【受験生必見‼】数Bの確率・統計分野(練習問題 正規分布編) | 知識の箱 (information-station.work)
二項分布の正規分布による近似
確率の最後として、二項分布の正規分布による近似という話をしていきます。二項分布B(n,p)に関して、下のことが成り立ちます。
二項分布B(n,p)に従う確率変数Xは、nが十分に大きいとき、近似的に正規分布N(np,npq)つまり、N(m,σ²)に従う。ただし、q=1-pとする。
これは、下の図のように、二項分布のグラフを書いて、nを大きくしていけばわかります。(サイコロをn回投げて1の目が出る回数をXとしたときの回数と確率の図。)
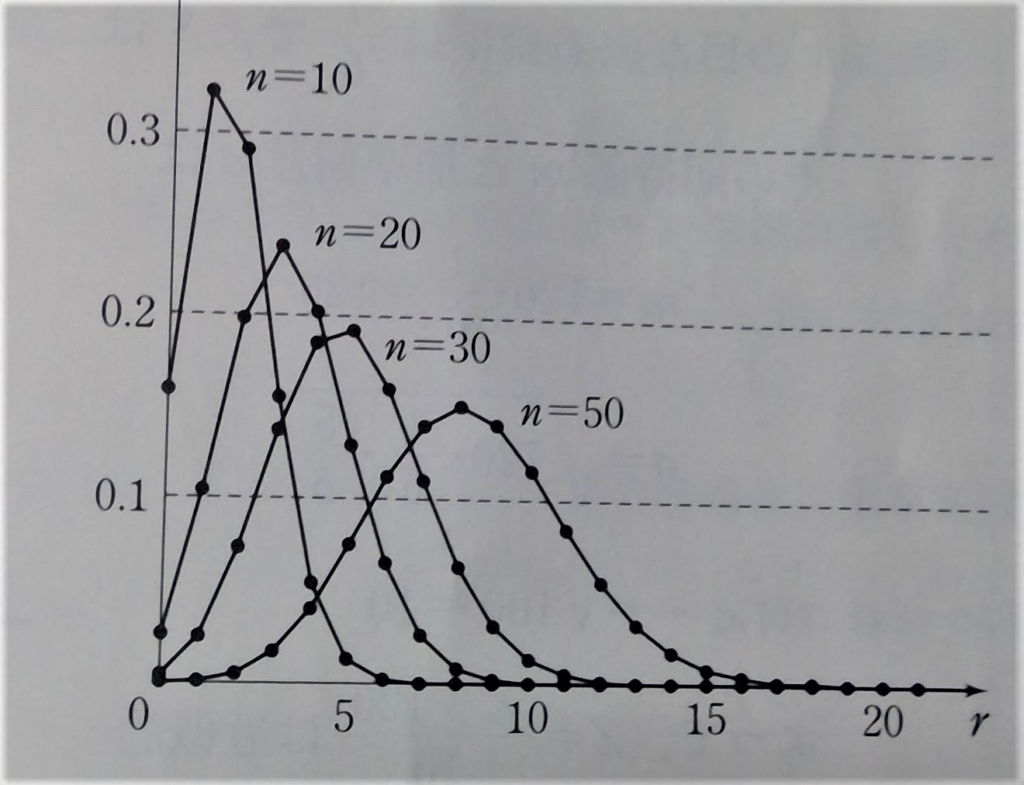
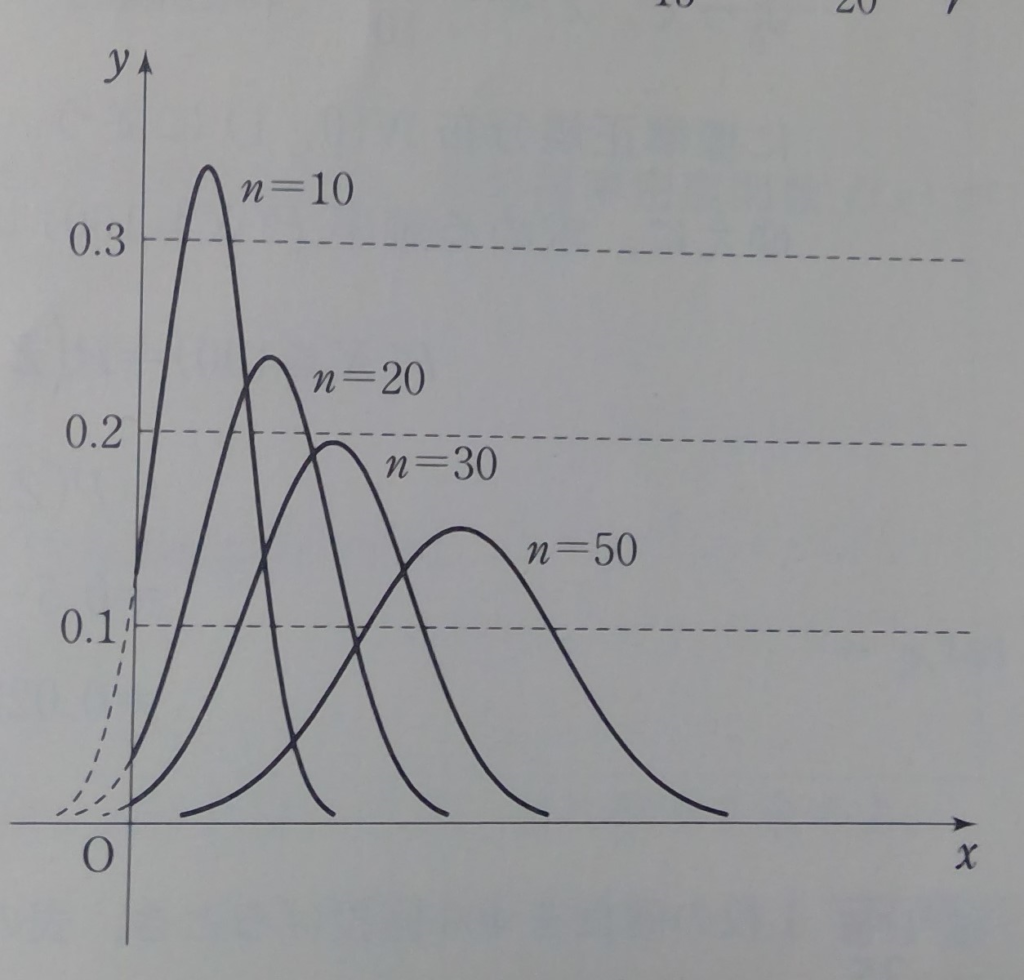
練習問題を解いてみたいという方は下のリンクをクリックして解いてみてください。
【受験生必見‼】数Bの確率・統計分野(練習問題 二項分布の近似編)
これで、確率の話は終わりです。
次は、統計の話をしていきます。
標本と抽出
統計的な調査には、調べたい対象全体の資料を集める全数調査と、対象全体から一部を抜き出して調べ、その結果から、全体の状況を推測する標本調査とがあります。
この標本調査では、調べたい対象全体集合を母集団、調査のために母集団から抜き出された要素の集合を、標本といいます。
さらに、母集団から標本を抜き出すことを標本の抽出といい、母集団、標本の要素の個数を、母集団の大きさ、標本の大きさといいます。
また、母集団の各要素を等しい確率で抽出する方法を無作為抽出、無作為抽出によってえらばれた標本を、無作為標本といいます。
この抽出において、毎回元に戻しながら次のものを1個ずつ取り出すことを復元抽出といい、これに対して、取り出したものを元に戻さずに続けて抽出することを非復元摘出と言います。
無作為抽出では、乱数さいや、乱数表(後ほど解説)が利用されます。ちなみにこの乱数さいというのは、正二十面体のサイコロで、0から9までの数字が2面ずつに書き込んであるもののことを言います。
先ほど紹介した乱数表というのは、0から9までの数をでたらめな順序に並べた大きな表で、上下、左右、斜めのいずれの並びをとっても、0から9までの数字が、大体等しい確率で現れるようになっています。
↓乱数表
| 52 | 37 | 82 | 80 | 69 | 38 | 55 | 92 | 37 | 98 | 55 | 34 | 68 | 96 | 79 | 83 | 90 | 75 | 62 | 52 |
| 27 | 46 | 79 | 56 | 84 | 45 | 12 | 18 | 87 | 38 | 73 | 59 | 45 | 20 | 76 | 48 | 83 | 71 | 16 | 97 |
| 74 | 65 | 97 | 88 | 74 | 58 | 91 | 36 | 40 | 34 | 82 | 46 | 63 | 33 | 15 | 65 | 34 | 36 | 38 | 49 |
| 54 | 62 | 97 | 19 | 16 | 76 | 24 | 43 | 22 | 92 | 71 | 54 | 55 | 72 | 97 | 33 | 74 | 33 | 22 | 71 |
| 66 | 99 | 24 | 81 | 49 | 98 | 52 | 99 | 79 | 44 | 78 | 17 | 43 | 90 | 66 | 82 | 58 | 73 | 61 | 17 |
| 38 | 45 | 62 | 12 | 14 | 63 | 12 | 85 | 85 | 99 | 29 | 75 | 95 | 37 | 31 | 43 | 82 | 55 | 81 | 91 |
| 26 | 38 | 85 | 96 | 34 | 81 | 86 | 96 | 87 | 65 | 79 | 50 | 46 | 83 | 51 | 99 | 45 | 58 | 46 | 96 |
| 89 | 80 | 19 | 54 | 36 | 72 | 75 | 33 | 78 | 12 | 90 | 70 | 53 | 22 | 16 | 16 | 51 | 42 | 48 | 72 |
| 98 | 55 | 50 | 36 | 40 | 44 | 31 | 55 | 39 | 43 | 53 | 22 | 85 | 25 | 45 | 84 | 76 | 29 | 32 | 75 |
| 92 | 97 | 60 | 80 | 40 | 34 | 58 | 40 | 78 | 70 | 74 | 21 | 46 | 84 | 24 | 97 | 76 | 85 | 75 | 77 |
| 65 | 65 | 58 | 84 | 65 | 65 | 30 | 92 | 50 | 93 | 63 | 35 | 42 | 46 | 19 | 12 | 59 | 43 | 89 | 87 |
| 93 | 78 | 80 | 83 | 94 | 92 | 83 | 86 | 66 | 22 | 98 | 45 | 66 | 90 | 52 | 27 | 70 | 78 | 40 | 35 |
| 55 | 48 | 39 | 49 | 75 | 28 | 25 | 22 | 47 | 43 | 89 | 13 | 86 | 76 | 99 | 72 | 86 | 91 | 85 | 71 |
| 96 | 42 | 53 | 14 | 58 | 26 | 82 | 85 | 39 | 95 | 15 | 20 | 28 | 85 | 59 | 65 | 68 | 18 | 36 | 38 |
| 90 | 77 | 84 | 86 | 55 | 68 | 64 | 67 | 94 | 34 | 28 | 34 | 29 | 47 | 83 | 82 | 32 | 83 | 79 | 36 |
| 16 | 52 | 23 | 43 | 39 | 70 | 65 | 48 | 74 | 73 | 13 | 36 | 51 | 27 | 33 | 44 | 16 | 45 | 22 | 46 |
| 42 | 65 | 31 | 41 | 32 | 64 | 97 | 43 | 84 | 39 | 29 | 78 | 98 | 29 | 15 | 47 | 83 | 36 | 41 | 69 |
| 68 | 84 | 69 | 17 | 64 | 22 | 77 | 13 | 25 | 83 | 46 | 75 | 28 | 28 | 30 | 76 | 49 | 46 | 89 | 46 |
| 66 | 33 | 27 | 23 | 49 | 74 | 76 | 69 | 13 | 43 | 98 | 97 | 16 | 29 | 78 | 79 | 30 | 61 | 85 | 65 |
| 74 | 50 | 67 | 92 | 80 | 81 | 47 | 39 | 83 | 41 | 62 | 56 | 68 | 78 | 15 | 84 | 37 | 19 | 12 | 57 |
↑引用元:10種類の乱数表
これについての練習問題も作ろうかなと思ったのですが、どうせ入試にも出ないし、生活において役に立つタイミングも1秒もないので、やめておきます。
次は、母集団分布という話をしていきたいと思います。
母集団分布
先ほど標本調査の話をしましたが、実際、統計調査で調べるのは、母集団に属する要素についての資料ですが、その資料は、ある変量の値の集合として表現できることが多いです。
ここで、大きさNの母集団において、変量xの異なる値を、x1,x2,…xnとし、それぞれの値を取る度数、すなわち、要素の個数を、f1,f2,… fnとする。
この時、母集団における変量xの分布を母集団分布,その平均値を母平均,標準偏差を、母標準偏差という。(確率の話でいう確率変数、期待値、標準偏差と同じような扱いだと思ってください。)
また、平均値mおよび、標準偏差σは下の式で与えられます。
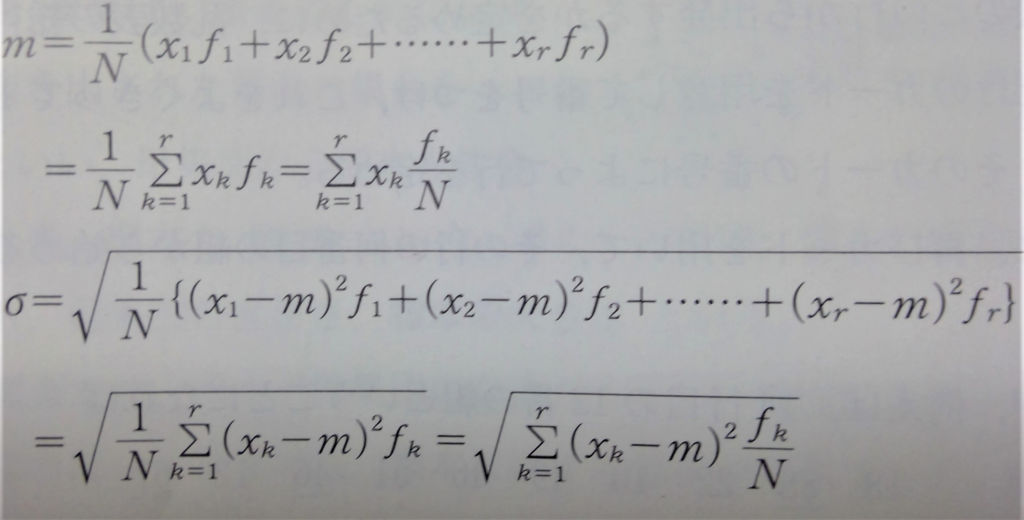
めんどくさい表現をしていますが、結局、確率変数が変量に、確率が度数になっただけだと思ってくれれば大丈夫です。
なので、大きさ1の無作為標本における変量xの値Xは、母集団分布に従う確率変数で、その期待値、標準偏差は、それぞれ、母平均、母標準偏差と一致します。
説明だけされても分からなかったのではないかと思うので、練習問題を解いて理解を深めましょう‼‼(下のリンク)
【受験生必見‼‼】数Bの確率・統計分野(練習問題 母平均、母標準偏差編)
標本平均の期待値と標準偏差
母集団から大きさnの標本を無作為に抽出し、変量xについて、その標本の持つxの値を、X1,X2,…Xnとするとき、
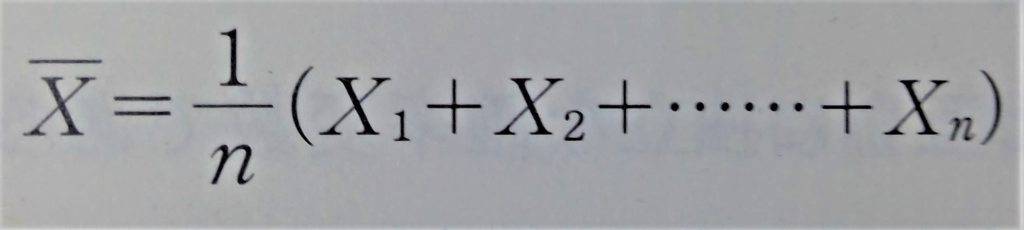
を標本平均といい、(母平均と同じ式なので、当然、値は母平均と等しくなります。)
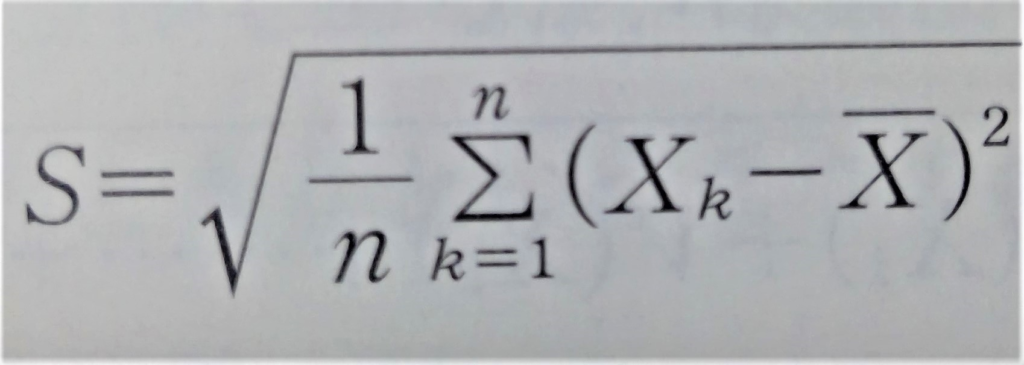
を標本標準偏差といいます。
また、母平均m、母標準偏差σの母集団から大きさnの無作為標本を抽出し、その標本の持つ変量xの値として定まる確率変数を、X1,X2,…Xnとする。この抽出が復元抽出の時、これらの各変数は、大きさ1の標本の確率変数とみなされ、それぞれ母集団分布に従うため、
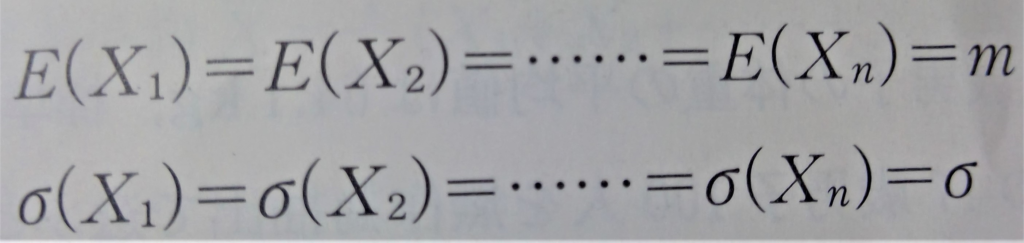
となります。
よって、標本平均の期待値および標準偏差は下のようにして求められます。
重要‼‼
↓期待値
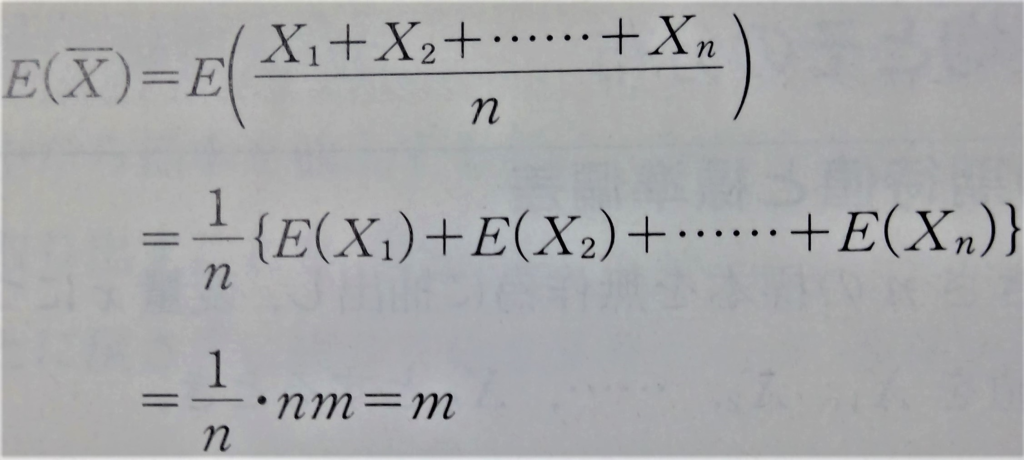
↓標準偏差(X1,X2,…Xnが互いに独立であることを利用します。)
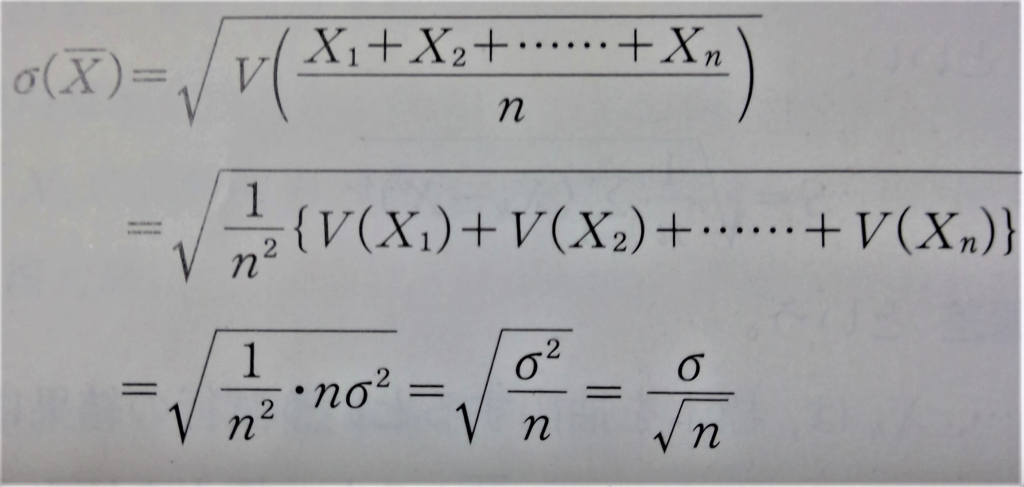
練習問題を解いてみたい方は下のリンクをクリック‼‼
【受験生必見‼‼】数Bの確率・統計分野(練習問題 標本分布の期待値と標準偏差編)
標本平均の分布と正規分布
母集団全体の中で特性Aを持つ要素の割合を、母比率、これに対して、標本の中で特性Aを持つ割合を、特性Aの標本比率という。
特性Aの母比率がpである十分大きな母集団から、大きさがnの標本を無作為に抽出するとき、標本の中で特性Aを持つものの個数をTとすると、Tは二項分布B(n,p)に従います。
これにより、確率の時と同様に、nが十分に大きいとき、Tは、近似的に、正規分布N(np,npq)に従います。
また、これを標本平均の分布についても応用させることで、下のようにいえます。
母平均m,母標準偏差σの母集団から大きさnの無作為標本を抽出するとき、標本平均は、nが十分に大きいならば、近似的に正規分布N(m,σ²)に従うものとしてみなすことができる。
また、これを応用したものとして、大数の法則などが挙げられます。
練習問題を解いてきちんと理解を深めましょう‼‼(下のリンク)
【受験生必見‼】数Bの確率・統計分野(練習問題 標本平均の近似編)
本人のやる気がパッとあがる【家庭教師の銀河】母平均の推定
先ほど述べた通り、母平均m、母標準偏差σを持つ母集団から摘出された大きさnの無作為標本の標本平均は、nが十分に大きいならば、近似的に正規分布N(m,σ²/n)に従います。
よって、確率の時と同様に、
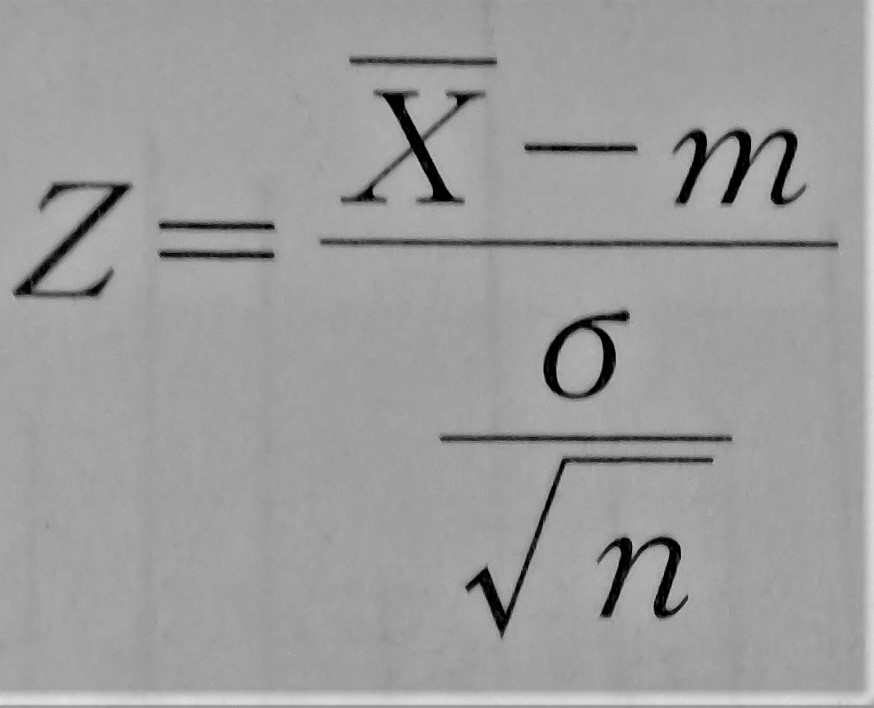
は、近似的に標準正規分布N(0,1)に従います。
また、この時、|Z|が、1.96以下である確率P(|Z|≦1.96)は、上の正規分布表を用いることで、下のことが導き出せます。
P(|Z|≦1.96)≒0.95
これを置き換えることで、
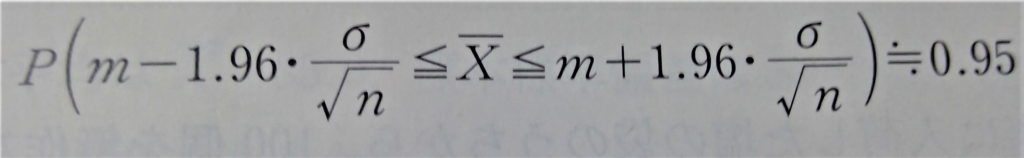
よって、

この式は、区間
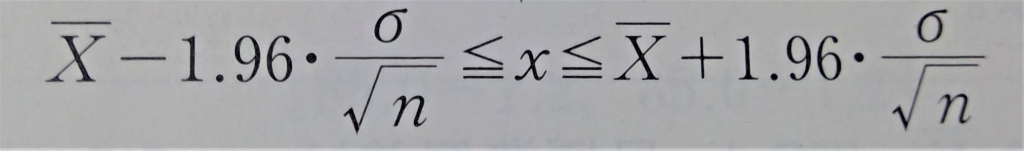
が、mの値を含むことが約95%の確からしさで期待できることを示しています。この区間を、母平均mに対する信頼度95%の信頼区間といい、下のように表されます。
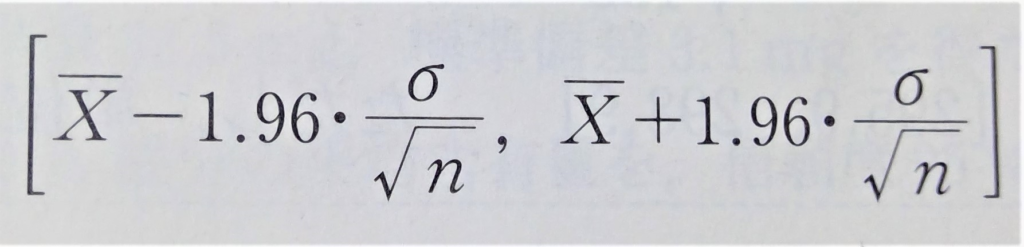
以上のことから、下のことが導き出されます。(厳密ではありませんが、こういうものだと思ってください。)
標本の大きさnが十分に大きいとき、母平均mに対する信頼度95%の信頼区間は、
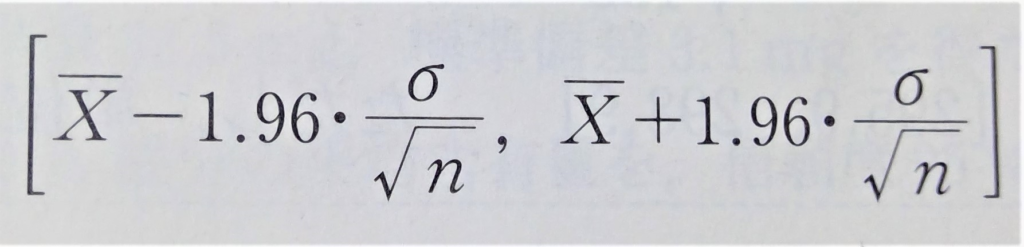
である。
これは、母平均がmである母集団から、無作為抽出を100回繰り返したときに、mを含む抽出が大体95回ぐらいあるということを意味しています。
説明だけされてもよくわからなかった方もいると思いますので、練習問題を解いてしっかり理解を深めましょう‼‼(下のリンク)
【受験生必見‼‼】数Bの確率・統計分野(練習問題 母平均の推定編)
母比率の推定
統計の最後の話として、母比率の推定という話をしていきます。
特性Aの母比率がpである十分大きな母集団から、大きさがnの標本を無作為に抽出するとき、標本の中で特性Aを持つものの個数をTとすると、標本比率Rについて、R=T/nが成り立ちます。(定義より自明。)
このとき、Rの期待値と分散は、標本平均の時と同様に、
- E(R)=(1/n)×E(T)=p
- V(R)=(1/n²)×V(T)=pq/n
と求められます。(Tが二項分布B(n,p)に従うことから簡単に導き出すことができます。)
よって、標本比率Rは、近似的に正規分布N(p,pq/n)に従います。(ただし、q=1-p)
これを先ほどの母平均の推定の話と同じようにすることで、下のことを導き出すことができます。(これの証明については、母平均の推定の定理のところをちょっと置き換えて変形するだけなので割愛させていただきます。)
標本の大きさnが十分に大きいとき、標本比率をRとすると、母比率pに対する信頼度95%の信頼区間は、
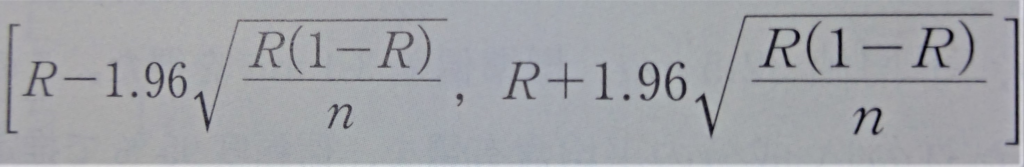
となります。
練習問題を解いてみたいという方は、下のリンクをクリックして解いてみてください。
【受験生必見‼‼】数Bの確率・統計分野(練習問題 母比率の推定編)
終わりに
お疲れさまでした‼‼
最終の腕試し問題として、2021年の大学入試共通テストの、確率・統計に関する問題です。よかったらどうぞ。簡単に解けるぐらいの実力はついていると思います。
たぶんこの記事一つ読むだけで数Bの確率・統計が理解できたと思います。この記事の引用元について気になる方は、下の広告をクリックしてください。
ほかにも面白い記事がたくさんありますので、そちらのほうも見ていただければ光栄です。
それでは次の記事で‼‼
 | 高等学校 数学B 高校用 文部科学省検定済教科書 [数B331] 第一学習社 価格:2,200円 |



プロフィール
このブログの情報が少しでも役に立てれば嬉しいです。