＼超わかりやすい‼／日本数学オリンピック本選2020全問解説‼

初めに

今回は、数学オリンピック2020本選の問題の解答・解説をしていきたいと思います‼‼

ノーヒントで解いてみたいという方は、下のリンクをクリック‼‼

第30回(2020年)JMO本選の問題 (imojp.org)

また、この記事の最後に、「数学オリンピックの問題を解けるようになる方法」について解説していますので、興味がある方はそちらのほうも読んでいただければ光栄です。

それでは日本数学オリンピック本選2020の解答・解説を見ていきましょう‼‼

日本数学オリンピック本選2020　解答・解説　問1

問題：

2以上の整数に対して定義され2以上の整数値を取る関数ｆであって、任意の2以上の整数ｍ,ｎに対して、

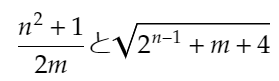
がともに整数となるような正の整数の組(m,n)を全て求めよ。

解答・解説：

まず、

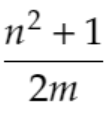
が整数になるということから、nは奇数であることは容易に導くことができます。

そのため、n=2k+1とあらわすことができます。また、これを代入することで、

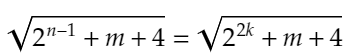
となります。また、mが正の整数という条件から、

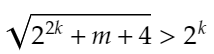
が導かれます。このとき、上の不等号の左辺は整数なので、下のように変形することができます。

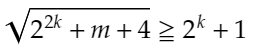
また、上の不等号の両辺はどちらも０以上なので、両辺を２乗することができるため、下のように変形することができます。

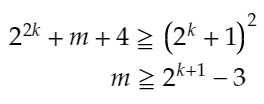
さらに、

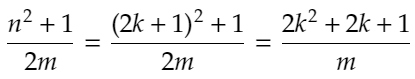
が整数という条件から、自明ですが、

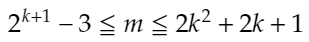
となるため、先ほど導いたことから、

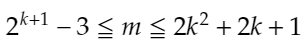
が導かれます。ここからは簡単で、左側が指数関数で、右側が２次関数(数学オリンピック頻出！)だから、絶対に交わる点があります。実際にグラフを書くと、下のようになります。

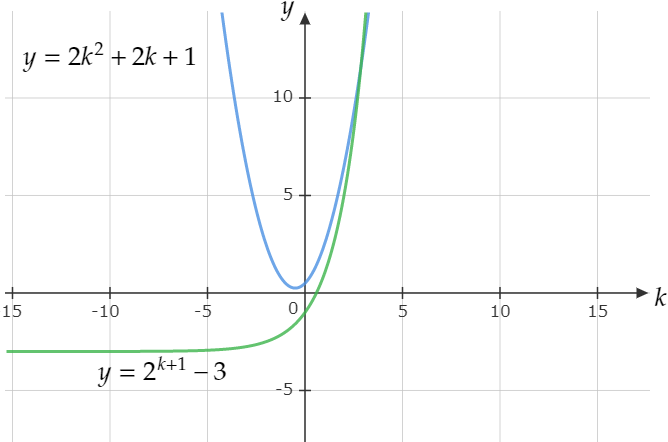
nが正の整数という条件から、kは0以上であり、交点の座標は、5より大きく6よりも小さいから、結局、

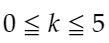
が導き出されます。

よって、nが11以下の正の奇数と分かるため、順番に試していったらmを求めることができます。(ここでは省略させていただきます。)

以上より、答えは、

(n,m)=(3,1),(11,61)

であることがわかります。

日本数学オリンピック本選2020　解答・解説　問2

問題：

BC＜AB,BC<ACなる⊿ABCの辺AB,AC上にそれぞれ点D,Eがあり、BD＝CE＝BCを満たしている。直線BEと直線CDの交点をPとする。⊿ABEの外接円と⊿ACDの外接円の交点のうち、Aでない方をQとしたとき、直線PQと直線BCは垂直に交わることを示せ。ただし、XYは線分XYの長さをあらわ明日ものとする。

解答・解説：

図を描くと、下のようになります。

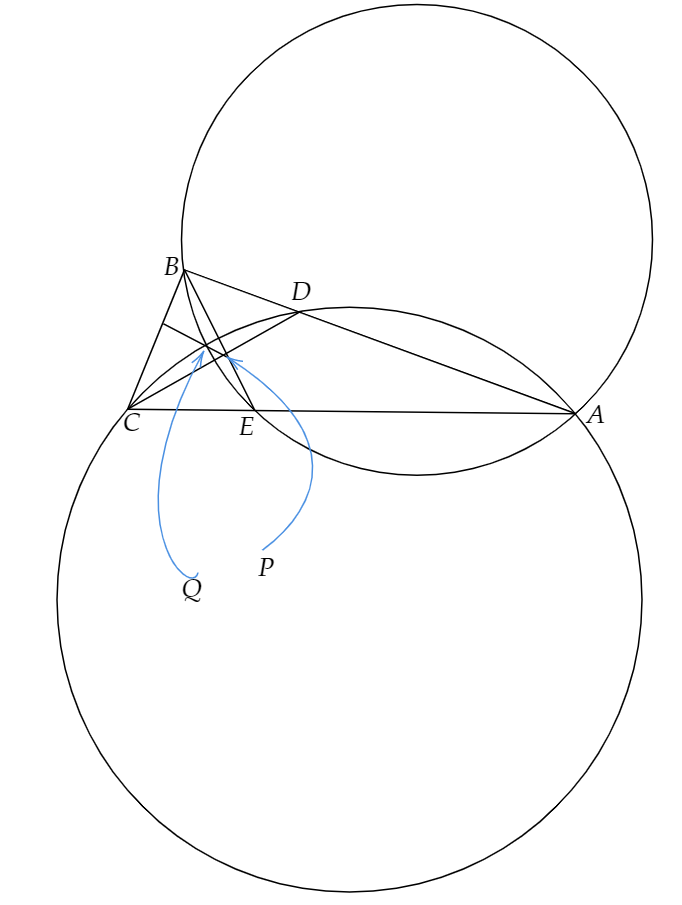
これは、気付くべきところき気づければ簡単です。円に内接する四角形の性質より下の角度が等しくなっていることがわかります。

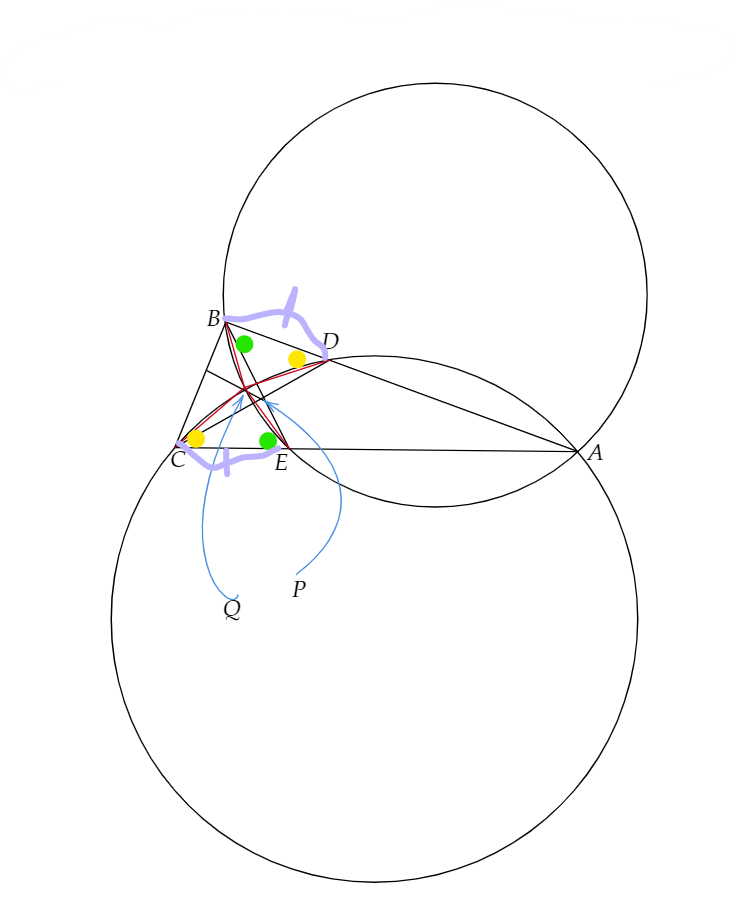
上の図から、⊿BQD≡⊿EQCより、BQ=QE、CQ=QDがわかります。さらに、問題の条件より、BC=CE,BC=BDであることがわかっているので、BQとCDは垂直で、CQとBEも垂直であることがわかります。

よって、Qは⊿BPCの垂心であることが導き出されるので、PQとBCが垂直であることがわかります。

これで、証明完了です。

日本数学オリンピック本選2020　解答・解説　問3

問題：

正の整数に対して正の整数値を取る関数ｆであって、任意の正の整数m,nに対して

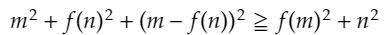
を満たすものを全て求めよ。

解答・解説：

こういう問題が出たときは、大体、代入するか、帰納法、漸化式で求めることが多いです。(一部例外や超応用させるものもあるけど…)

まずは、手っ取り早い「代入」をやってみるといいです。

mとnに異なる値を入れても、式がややこしくなるだけだし、mとnに同じ値を入れても、

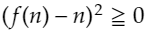
といった風になって、全然話が進みません。

次は、「帰納法でどうにかならないかな」と思って手を動かしてみます。

そもそも、帰納法を使うんだったら、関数に対して、それの値や範囲を制限できる数がないと難しいです。

しかし、先ほど代入しても全く手ごたえがなかったことから、関数の値に対してある数が制限をかけているというのはなかなかなさそうです。

ここで、問題文に戻ってみます。

「 正の整数に対して正の整数値を取る 」なので、すべての関数ｆの値は1以上の整数ということを表しており、これが唯一今わかっている、この関数にかけられる数の制限です。

だから、ここから切り口を開いていきたいと思います。

帰納法を関数ｆを定める手がかりとして使うなら、

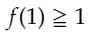
を一般化するのが一番最初に思いつくやつだと思うので、

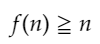
が成り立つものと仮定します。

この時、 m=k、n=k+1を代入します。すると、

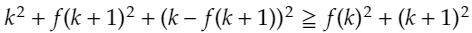
がわかります。これをさらに変形することで、

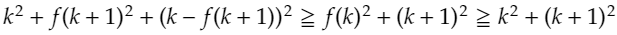
となります。これをさらに変形させると、下のようになります。(f(k+1)でまとめる形にする。)

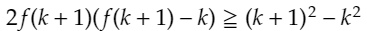
ここで大体の人はの手が止まるかと思います。

私もここで結構手が止まりました。いったん、基本に戻ってみます。証明したいことは

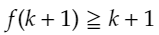
です。これは、この問題では、

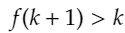
と同値なので(kは整数だから。)、これを示せばいいことがわかります。こう考えると簡単です。先ほどの不等式は、

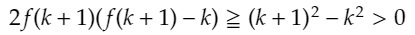
と変形することができるため、

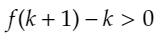
が導かれます。

長くなってしまいましたが、帰納法より、

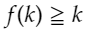
と分かります。(この証明だとちょっと抜けているところがあるので、足りない言葉は適当に埋めておいてください。)

次は、漸化式に注目してみたいと思います。

「できるだけ代入して漸化式を作りやすくなるのはないかな」と思って試行錯誤していると、

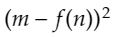
がめっちゃ邪魔だなと思い、これを消そうとすると、

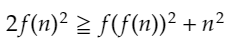
という形に行きつきます。

さて、「これをどう処理するか」という話ですが、漸化式として問題を解くためには、数列a_kを、tを正の整数として、

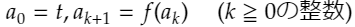
と定めることが最適だといえます。

上の数列の条件より、先ほどの不等式は、結局、nにa_kを代入することで、

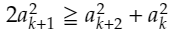
と変形できます。

また、ここで、先ほど帰納法により導いたことを使うと、

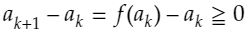
であることは容易にわかります。また、上のような漸化式は、

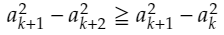
と変形することができます。「次数を下げられないかな」と考えると、ちょうど2乗ー2乗という形になっているので、先ほどの不等式を使うと、

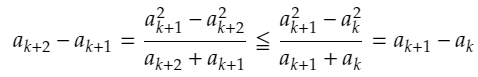
を導くことができます。この形を見たら、無限降下法がすぐに思いつくかと思います。

a_k+1>a_kとすると、a_k+1-a_kは正の整数なので、 a_k+1-a_k が最小となるようなkを取ることができます。

しかし、この時、

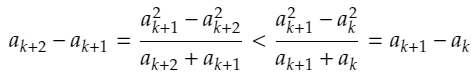
となるため、 a_k+1-a_k の最小性に矛盾します。(これが無限降下法。)よって、a_k+1=a_kであることが導き出されます。

ここまでわかったら超絶簡単です。先ほど導いたことから、f(x)=xとなる正の整数xを取ることができます。ここで、n=x,m=x+1を問題の不等式に代入すると、

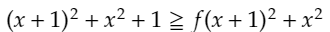
となるため、これをちょっと変形すると、

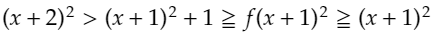
となり、

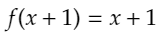
が導き出されます。(はさみうちの原理。)これを用いると、帰納的に、xより大きいすべての正の整数Lにおいて、

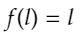
が成り立つことがわかります。

これと同様のことをxよりも小さい正の整数でも行いたいと思います。問題の不等式に、n=x,m=x-1を代入すると、

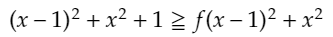
となります。これも先ほどと同様に変形すると、

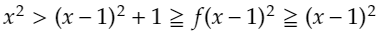
先ほどと同様に、はさみうちの原理より、

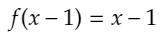
が導き出されます。よって、xより小さいすべての正の整数Lについて、先ほどと同じように、

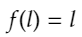
が成り立つことがわかります。以上より、関数ｆは、すべての正の整数nに対して、

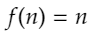
となる関数であることがわかりました。

(↑問題の不等式にこれを代入していただいたら、簡単に確認することができます。)

日本数学オリンピック本選2020　解答・解説　問4

問題：

nを2以上の整数とする。円周上に相異なる3n個の点があり、これらを特別な点と呼ぶことにする。A君とB君が以下の操作をn回行う。

＜操作＞

• まず、A君が線分で直接結ばれていない2つの特別な点を選んで線分で結ぶ。次に、B君が駒の置かれていない特別な点を1つ選んで駒を置く。

A君はB君の駒の置き方にかかわらず、n回の操作が終わったときに駒の置かれている特別な点と駒の置かれていない特別な点を結ぶ線分の数を(n-1)/6以上にできることを示せ。

解答・解説：

数学オリンピック本選の4番の中ではこのレベルだとかなりマシです。(難易度的には３番と変わらないかちょっと簡単かなというぐらい。)

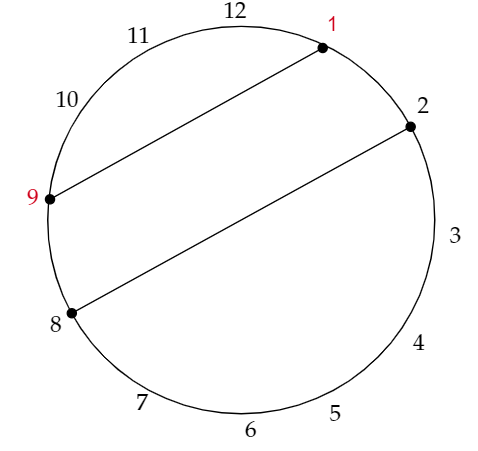
まず、実際に手を動かしてみるとわかりやすいです。例えば、まず、１回目の操作で下のようになったとします。(1を赤色にしているのは、1に駒が置いてあるという意味。)

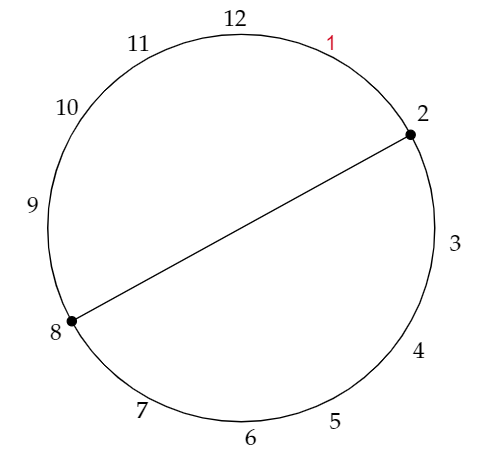
もし、Aが、駒が置いてないところ同士で結んでいったとしたら、BがAが結んでいないところに駒を置き続けた時に、 n回の操作が終わったときに駒の置かれている特別な点と駒の置かれていない特別な点を結ぶ線分の数を(n-1)/6以上にできなくなってしまうから、次は、1から線分を結ぶことにします。

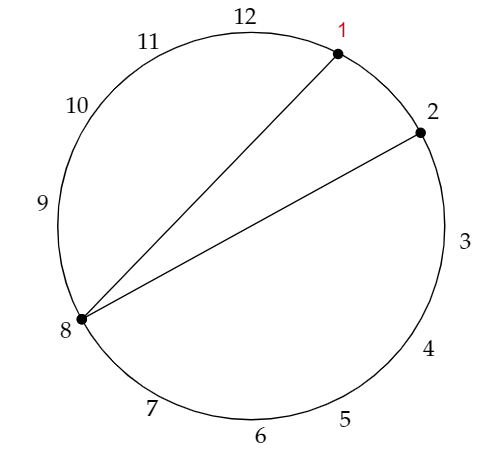
でも、適当に下のようにやっても、

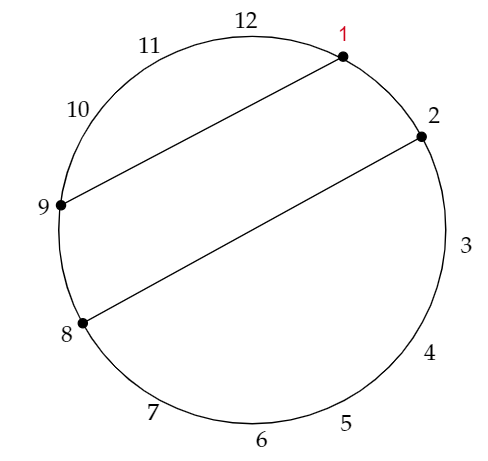
下のところにBが駒を置いた時に詰むので、

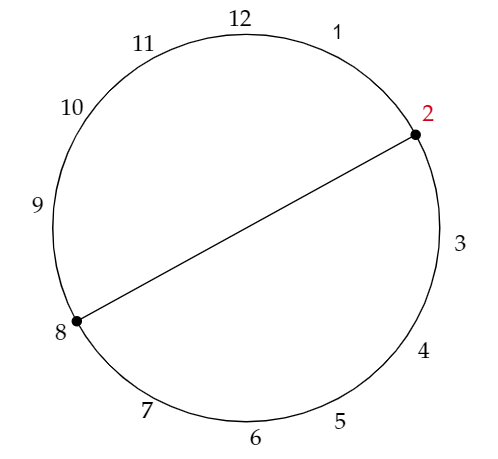
下のように線分で結びます。

この形はめっちゃ強いです。もし、上の2本を無効化(駒がある点と駒がない点を結ぶ線じゃなくすること。)しようと思ったら、Ｂは駒が2個も必要となってしまいます。かといって、駒は1個置いただけでは、全く効果がないので、これを作るだけで確実に1本は作れます。

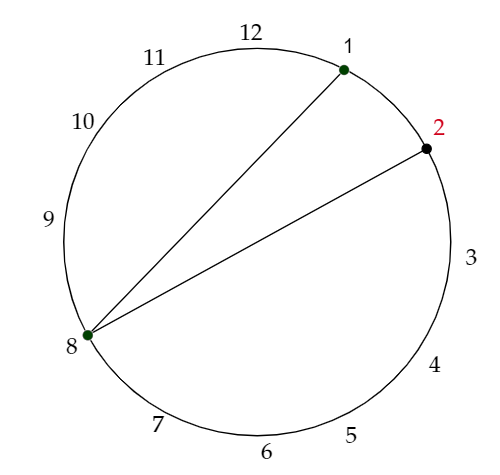
これは、最初にBが下のように点を置いたとしても、

下のようにすれば、さっきの形を作ることができるので、実質、Bが駒を置き終わったときに片方の端点に駒が置かれていない線分があったらいいことになります。

「これを繰り返すことでn回目には(n-1)/6本は作れるんじゃないの？」と予想を立てることができます。

当たり前ですが、これをそのまま真に受けて作っていっても、いたちごっこになるだけで、一向に増えるわけがありません。

この形は、「少なくとも一つの点に駒が置かれていない線分があるときに、線分を1本書くだけで確実に一本は問題の条件に合う線分を作ることができる」(証明でいいますが、厳密にいうとちょっと違います。)というのがミソです。

なので、「少なくとも一つの点に駒が置かれていない線分がいっぱいある状況を作ってから、この結び方をしたら、問題の条件を満たす」という証明の方針で証明していこうと思います。

分数でやるのはだるいので、n=6m+k(0≦k≦5)としてやってみたいと思います。

この場合は、m+1本以上あることを証明すればいいことになります。

逆からたどると、少なくとも一つの点に駒が置かれていない線分の数が2m+1以上になれば、Bがどんだけ頑張って無効化しようとしても、2m+1-(2m+1)/2 (あの形を消すには2個の点が必要なので。)以上は問題の条件を満たす線分があります。

さらに、少なくとも一つの点に駒が置かれていない線分の数が2m+1以上になるためには、最低でも、4m+1回は操作を繰り返さねければいけません。(4m+1回の時に4m+1-(4m+1)/2≦2m+1 本以上の線分ができるといえるから。)

こう考えると、n=6mと仮定したのは失敗です。

結局、大事なのは、2m+1と4m+1だけなので、6m+2をまとまりとしてみていきたいと思います。

ちゃんとした(？)証明

というわけで、改めて、n=6m+2+k(0≦k≦5)と仮定して証明に入っていきたいと思います。

最初のk回はどこに線を引いてもOKです。

次の4m+1回は、Aは「駒が置かれていない点同士をむすぶ。」という操作をするとします。

この時、少なくとも一つの点に駒が置かれていない線分が、4m+1-(2m+1)本、つまり、2m+1本は存在します。

そして、 少なくとも一つの点に駒が置かれていない線分を2m+1本選び、それらを、

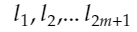
とします。

さらに、

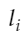
の端点のうち、駒が置いてない方をx、もう一つのほうの点をyとし、さらに、任意の駒が置いてある点をzとします。

次の2m+1回は次の操作を繰り返し続けることにします。

• yに駒が置いてあったときは、yとzを結ぶ。yに駒が置いてないときは、xとzを結ぶ。

これを繰り返したら、先ほどの形ができ、これを無効化するには、Bは2個駒が必要なので、問題の条件を満たす線分が、最低でも2m+1-(2m+1)/2=m+1本はあります。

よって、題意は満たされました。

超雑なので、解答欄にはこんな風には書けませんが、これで大まかな証明はできています。

日本数学オリンピック本選2020　解答・解説　問5

問題：

ある正の実数cに対していかが成立するような正の整数からなる数列 a₁,a₂,a₃, … を全て求めよ。

• 任意の正の整数m,nに対してgcd(a_m+n,a_n+m) > c(m+n)

ただし、正の整数x,yに対してxとyの最大公約数をgcd(x,y)で表す。

解答・解説：

答えの予想は誰でもつけられると思います。

数学オリンピックあるあるですが、f(n)を求めるやつとか、a_nを求めるやつとかは、問3がそうであったように、結構、f(n)=n+kとか、a_n=n+kとかが多いです。

実際に、 a_n=n+k (0≦k)とか定めたら、 gcd(a_m+n,a_n+m)＝n+m+k>n+mだから、あてはめても成り立ちます。

多分、ここまでだったら、誰でもできると思います。

でも、これが答えの一つと分かっても、「答えがこれだけ」と証明するのが全然できませんでした。

考えてもわからなかったので、下の本を見ることに…

答えを見たら、「あー」とはなりますが、「どっからその発想出てくるんだよ！」ってレベルだったので、この問題を初見で解いた受験生がもしいたら本当に尊敬します。

ちなみに、答えはあってました。でも、証明は全然わからなかったので、先ほど紹介した本に乗っていた解答をそのまま写させていただくことにします。

証明

d=a_n+1– a_nとします。ここで、d>0と仮定します。

そして、さらに、k>a_n/dとなる任意の正の整数kを取ります。

次に、nとkd-a_nを問題の不等式に代入します。

このとき、

gcd(kd,a_kd-an+n) >c(kd-a_n+n) (a_nがanとなっているのはソフトの都合上なので、ご容赦ください。)

が得られます。

同様に、n+1とkd-a_nも問題の不等式に代入します。

この時、

gcd((k+1)d,a_kd-an+n+1)>c(kd-a_n+n+1)

が得られます。

そして、次の補題を示します。

補題:

a,b,s,tを正の整数とする。sとtが互いに素の時、gcd(a,s)gcd(b,t)≦lcm(a,b)である。(lcmは最小公倍数のことを表すものとする。)

証明

この補題が思いつくかどうかはさておきとして、この補題自体の証明は簡単です。

素数pおよび、正の整数Nに対してNがp^kで割り切れるような最大の非負整数kをord_pNで表すとき、任意の素数pに対して、 ord_p gcd(a,s)gcd(b,t)≦ ord_p lcm(a,b) が成り立つことを示せばいいことになります。

また、sとtが互いに素であることから、絶対にどっちかはpで割り切れません。

なので、sがpで割り切れないものとします。

この時、 ord_p gcd(a,s)gcd(b,t) ＝ ord_p gcd(a,s)＋ ord_p gcd(b,t)＝ ord_p gcd(b,t) ≦ ord_p gcd(b) ≦ ord_p lcm(a,b) なので、題意は満たされました。

これで、補題の証明は完了です。

よって、nとn+1は互いに素なので、今証明した補題を使うことで、下のことが成り立ちます。

gcd((k+1)d,a_kd-an+n+1) gcd(kd,a_kd-an+n) ≦lcm(kd,(k+1)d)≦k(k+1)d

よって、十分大きい任意の整数kに対して、下のことが成り立つことが導かれます。

k(k+1)d > c²(kd-a_n+n)(kd-a_n+n+1)

上の式は十分大きい任意の整数kに対して成り立つことから、k²の係数に注目して、下の不等式が成り立つことがわかります。

d≧c²d²

今、d≧0と仮定しているので、これは、

d≦c^-2

が成り立つことと同値です。

また、d<0の場合も、同様にして、

-d≦c^-2

が成り立つことがわかるため、結局、

|d|≦c^-2

が成り立つことがわかりました。

ここまで来たら、あとは楽です。

まず、nとn+1に対して、問題の不等式を用いると、

• gcd(a_n+n+1,a_n+1+n)>c(2n+1)

が得られます。

ここで、a_n+n+1 ≠ a_n+1+n と仮定すると、 gcd(a_n+ n +1,a_n+1 + n)≦| a_n+1– a_n -1|≦c^-2+1より、先ほどのを使うと、c^-2+1>c(2n+1)であることが導かれます。

なので、 c^-2+1≦c(2n+1)の時、つまり、nが十分に大きい整数の時、 a_n+n+1 = a_n+1+n となります。

もし、a_m≠m+dとなるmが存在したとします。この時、十分に大きい整数nと、先ほどのmを問題の不等式に代入すると、

c(m+n) < gcd(a_m+n,m+n+d) ≦ |a_m – m – d|

となり、矛盾します。

よって、a₁が正の整数であるという条件から、a_n=n+d(d≧0)と書けることがわかります。

この問題は、答えの予想は簡単にできるんですが、証明がかなり難しかったと思います。

特に、kを使って多項式の不等式みたいな形にするのがとても発想力が必要になると思います。

これで、問題の解説は終了です。

ほかの年の問題の記事や、予選とかの問題の解説をしている記事もありますので、そちらの方も見ていただければ嬉しいです。

また、数学オリンピックの問題を解けるようになりたい方は、ぜひ、下のところを読んでください‼‼

数学オリンピックの問題を解けるようになるには

正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか本選の最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。

というわけで、数学オリンピック対策でぜひ読んでおくべき本を紹介したいと思います‼‼

パーフェクトマスターシリーズ

これは、特定の分野をしっかり固めたい方にお勧めです。

大事な問題だけがセレクトされているので、その分野の問題をしっかり鍛えることができます。

初等整数を鍛えたい方にオススメ‼‼

これは、初等整数をマスターしたい方にお勧めです。

初等整数の問題はよく本選の大門１なんかで出題されることが多いので、そういった類の問題を解けるようになりたい方はこの本がおすすめです‼‼

平面幾何を鍛えたい方にオススメ‼‼

下の本は平面幾何を鍛えたい方にオススメの本です。

「数学オリンピックの幾何の問題を解いていると、「こんな発想が出てくるわけないだろ！！」みたいな問題にあたることはよくあると思います。

この本を読むことで、そういう問題たちをすらすら解けるようになります‼‼

代数・解析を鍛えたい方にオススメ‼‼

下の本は、代数、解析を鍛えたい方におススメの本です

数学オリンピックの問題の中でも、「絶対解けるか！！」みたいなレベルの問題って稀にあるじゃないですか。

こういう問題は、代数・解析の分野に入ることが多いです。

数学オリンピックで、難しい問題を解いてほかの受験生と差をつけたい方にはこの本をお勧めします‼

組み合わせ論を鍛えたい方にオススメ‼‼

下の本は、組み合わせ論を鍛えたい方におススメの本です。

数学オリンピックの場合の数の問題は、ほかの分野に比べてそこまで難しい問題が出題されることはあまりないんですが、とにかくめちゃくちゃミスしやすいように巧妙に仕組まれています。

そんなミスしやすいポイントをしっかり克服するためにも、ぜひこの本は見ていただきたいです。

過去問をひたすら解きまくる

これも結構おすすめです。過去問を全部解いていれば、実質数学オリンピックに関係する問題を全部網羅したようなものなので、完璧にマスターしたい方にはこちらの方法をお勧めします‼‼

ほかにも過去問についてはいろんな著者がいろんな本を出版しているので、ぜひそちらの本も調べてみてください。(下リンク)

Amazon.com

数学オリンピックの参考書は高すぎる‼‼

今紹介させていただいた本を見て思ったかもしれませんが、とにかくこういった類の参考書は高いです。

でも、なんと「kindle Unlimited」なら、今紹介した本が月額980円払うだけでで読むことができます‼‼‼

1冊読むだけで余裕で元を取れますね。

さらに、今だけ初月無料なので、初月だけ契約すれば、本当に1銭も払わず、あの高額な本たちを読むことができます😎

私もこれを使っていて、「kindle Unlimited」なら、大体の本が無料で読めちゃうので、知りたいことがあったら簡単に本で調べたり、本で勉強したりすることができます。

また、息抜きに読書したいときにも役に立つので、ぜひこれは、お勧めしたいです‼‼

↓興味がある方はこちら‼‼

終わりに

いかがでしたか。

ほかにも数学オリンピックの解説している記事もありますので、そちらのほうも見ていただければ光栄です‼‼

それでは次の記事で‼