＼良問揃い‼／JMO予選2021全問解説‼‼

初めに

前回に引き続き数学オリンピック予選2021の解説をしていこうと思います‼‼

本記事では問9から問12までなので、ほかの問題の解説が気になる方は、下のリンクをクリック‼‼

また、この記事の最後のほうでは、「数学オリンピックの問題を解けるようになる方法」について解説しているので、ぜひ、そちらのほうもチェック‼‼

【超わかりやすい‼‼】数学オリンピック予選2021全問解説‼

数学オリンピック予選2021の問題を全問解説していこうと思います‼‼わからない問題があった方や、解説を読んでも意味が分からなかった方は、誰でも簡単にわかるように超わかりやすく解説しているので、ぜひ読んでみてください。ちなみに、この記事では数学オリンピック2021予選の問1、問2、問3、問4を解説します。

information-station.work

【目指せ本選‼】超わかりやすい日本数学オリンピック予選2021全問解説

数学オリンピック予選2021の問題を全問解説していこうと思います‼‼わからない問題があった方や、解説を読んでも意味が分からなかった方は、誰でも簡単にわかるように超わかりやすく解説しているので、ぜひ読んでみてください。ちなみに、この記事では数学オリンピック2021予選の問5、問6、問7、問8を解説します。

information-station.work

それでは、日本数学オリンピック予選2021の問題の解答＆解説を見ていきましょう‼‼

＼“プログラミング”が数学力を金に変える‼／

プログラミングの無料体験はこちら‼‼

↑必要なのは名前とメアドだけ,顔出し不要,完全オンライン完結‼

問9:

問題:2021×2021のまず目の各マスに1，2，3の数を一つずつ書き込む方法であって、どの2×2のマス目についてもその4マスに書かれている数の総和が8になるよううなものが全部でA通りあるとする。この時、Aを100で割ったあまりをもとめよ。

解説:この問題は解法が分からなかったので、数学オリンピック公式の解答を書いておきます。

まず、1≦i≦2021、1≦j≦2021に対して、上から、i行目、左から、j列目のマスを、(i,j)と表し、(i,j)に書き込まれた数をf(i,j)で表します。さらに、

g(i,j)＝f(i,j) (i+jが偶数の時)
g(i,j)＝4-f(i,j) (i+jが奇数の時)

と定めます。この時、1≦i≦2020、1≦j≦2020に対して、f(i,j)+f(i+1,j)+f(i,j+1)+f(i+1,j+1)=8であるから、i+jが偶数と奇数の時に場合分けして計算すると、どちらも場合でも、

g(i+1,j)-g(i,j)=g(i+1,j+1)-g(i,j+1)…①

となることが分かります。

また、①を満たすg(i,j)は、問題の条件を満たすから、このようなg(i,j)をもとめることと問題を解くことは同値であることがわかります。

ここで、g(1,1)…g(1,2021)の最大値、最小値をそれぞれ、M,mとし、さらに、①の値を,xとします。

この時、g(i,j)が1~3の整数となるための必要十分条件は、1≦m＋xかつ、M+x≦3つまり、1－m≦x≦3－Mです。

もし、g(1,1)…g(1,2021)の値がすべて決まっていたら、xの値を入れることで、すべての場所の値が決まるから、g(1,1)…g(1,2021)の値がすべて決まっている場合における通り数は、(3+m-M)^2021とわかります。(xの変動域を考えればいい。)

ここで、M-mの値の場合分けをしていきます。

M-m＝0の時
g(1,1)…g(1,2021)の値の決め方は3通りだから、求める通り数は3^2021通りです。

M-m＝1の時
g(1,1)…g(1,2021)の決め方は、2^2021－2(全部同じ数字になってしまうからー2)通りだから、求める通り数は、2^4042-2^2022通りです。

M-m=2の時
g(1,1)…g(1,2021)の決め方は、3^2021-2×(2^2021-2)-3通りだから、求める通り数は
3^2021-2×(2^2021-2)-3通りとわかります。

よって、以上のすべての場合の通り数を足し合わせることにより、
A=3^2021＋2^4042-2^2022＋3^2021-2×(2^2021-2)-3通りであることが分かります。よって、これを100で割ったあまりをもとめればいいことが分かります。

まず、Aを4で割ったあまりは、3を4－1と置いて、二項定理を使うことで３であることが分かります。

次に、Aを25で割ったあまりは、オイラーの定理(https://information-station.work/337)
を使うことで、3とわかります。

よって、求めるAを100で割ったあまりは3であることが分かります。

これは私の中で一番難しかった問題だと思います。通り数が分かるところまで行っても、そこから100で割ったあまりをもとめるところが難しいと思います。

＼プログラミングで数学力が生かされる‼／

プログラミングの無料体験はこちら‼‼

↑必要なのは名前とメアドだけ,顔出し不要,完全オンライン完結‼

問10:

三角形ABCの辺AB,AC上に点D,Eがあり、4点D,B,C,Eは同一円上にある。また、四角形DBCEの内部に点Pがあり、∠BDP＝∠BPC=∠PECを満たしている。AB=9,AC=11,DP=1,EP=3の時、BP/CPの値を求めよ。(下の図の長さ,角度はちょっとおかしいです。)

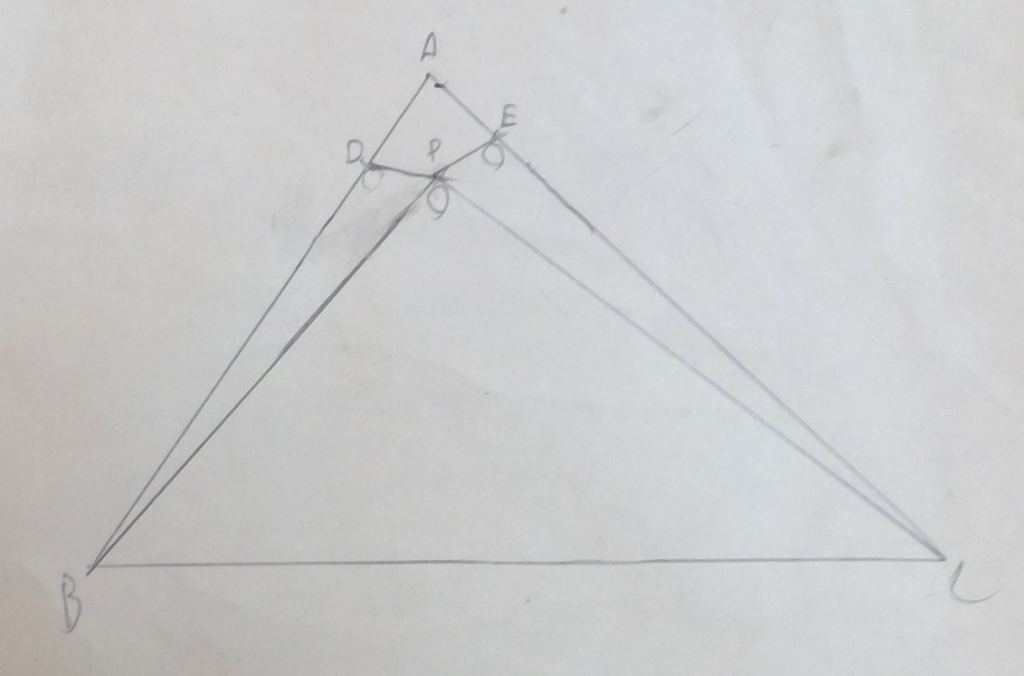
まず、下の図のように点Q,R をとります。

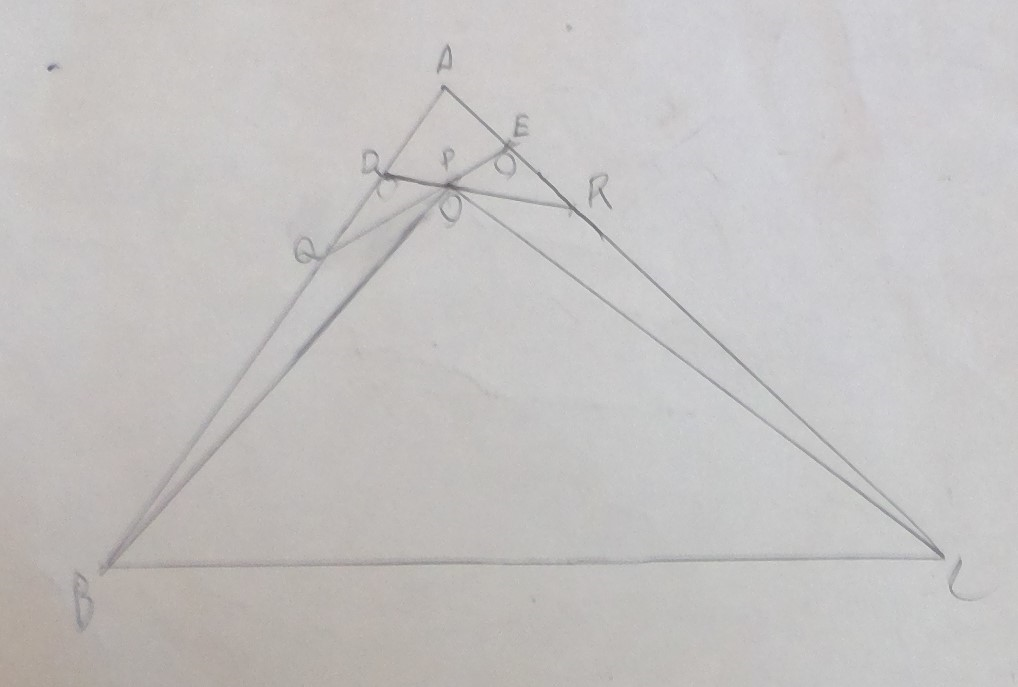
この時、外角定理より、下の図のようになるので、⊿BQP∽⊿PRCとわかります。

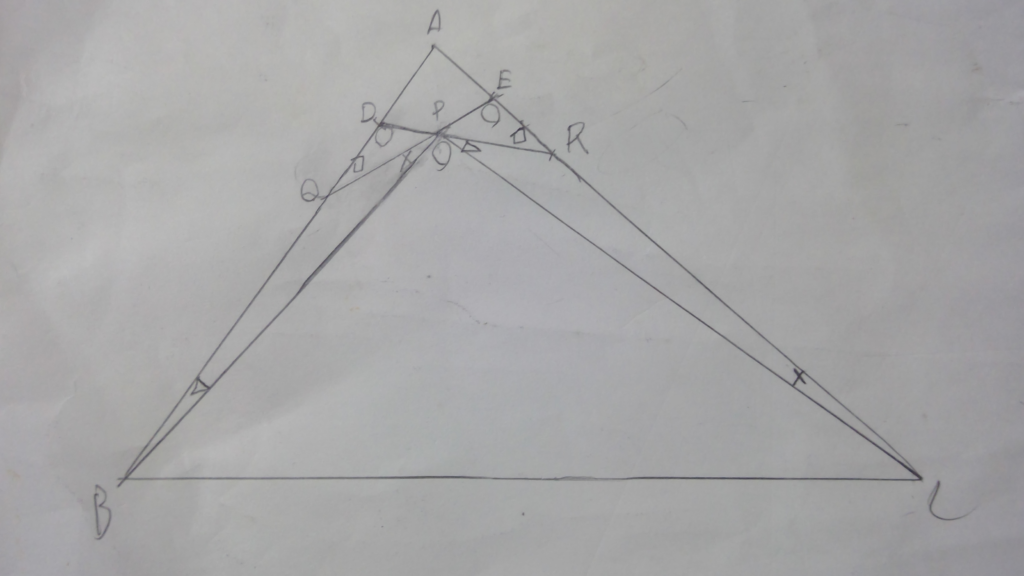
また、円周角の定理より四点D,Q,R,Eは共円であることが分かるので、上の図のように⊿DQP∽⊿ERPであることが分かります。また、四点D,B,C,Eも共円であるから、BCとQRは平行であることが分かります。←円に内接する四角形の性質より明らか。

以上のことを使うと、
CP^2/BP^2=BQ×QP/CR×RP=(9/11)×(1/3)=3/11とわかるので、求める答えは、√33/11であることが分かります。

問11:

1以上1000以下の整数からなる組(x,y,z,ω)すべてについて、xy+zω,xz+yω,xω+yzの最大値を足し合わせた値を、Mとする。
　同様に、1以上1000以下の整数からなる組(x,y,z,ω)すべてについて、xy+zω,xz+yω,xω+yzの最小値を足し合わせた値を、mとする。
M-mの正の約数の個数を求めよ。

3つの実数a,b,cにおいて、最大値と最小値の差は、

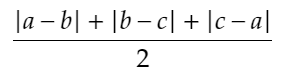
であることに注目します。

このa,b,cを、xy+zω,xz+yω,xω+yzに置き換えると、M-mの値は、

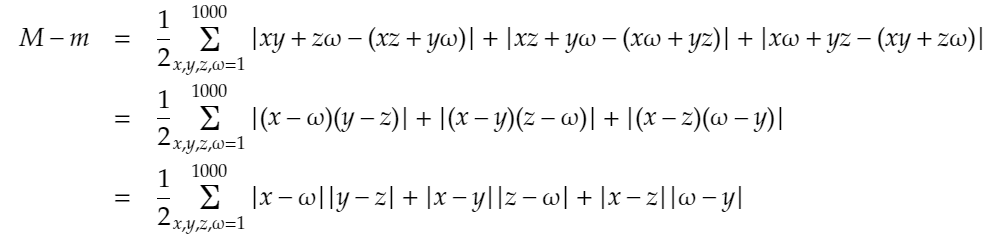
となります。また、文字が変わっても値は変わらないので、

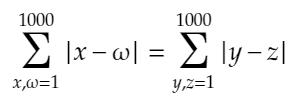
となります。さらに、結局4つの変数の値を1から1000まで変化させているだけなので、

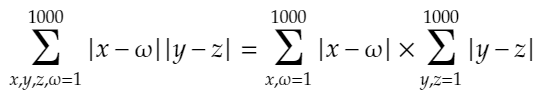
であることがわかります。この二つのことから、先ほどのやつを、さらに下のように変形することができます。

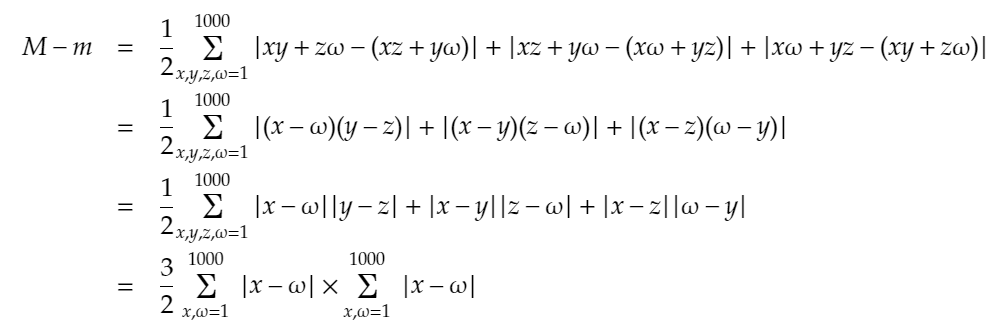
ここまで来たら後は簡単です。

「二変数の級数の和」と思うと難しそうかもしれませんが、イメージさえしっかり持てば、簡単に理解できます。

x>ωで、xとωの値を1から1000まで変化させると、|x-ω|の値は、下のように変化します。

これを見ると、1が999個、2が998個、3が997個…999が1個という風になっているので、最終的には、下のように変形することができます。

※2倍しているのは、xとωの大小関係が逆の時を考慮するためです。

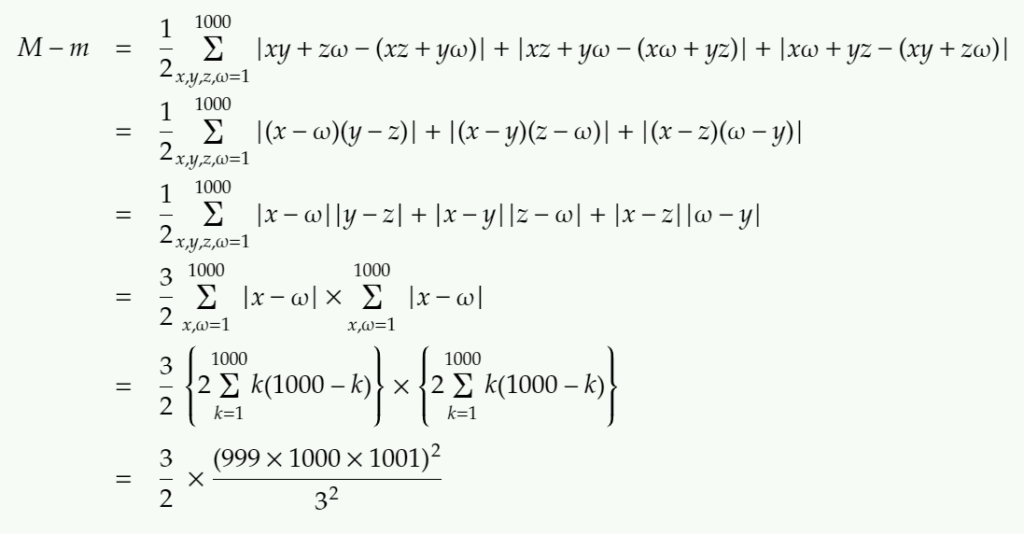
よって、最終的な結果として出てきた、3/2×(999×1000×1001)²/3²の約数の個数を求めればいいので、

M-m = 3/2×(999×1000×1001)²/3² = 2⁵×3⁵×5⁶×7²×11²×13²×37²

より、これの約数の個数は、

6×6×7×3×3×3×3

で求めることができるため、最終的に答えは、20412個と分かります。

問12:

この問題は、問題を打つことが大変なので、問題は掲載しません。

↓問題はこちら‼‼

第31回(2021年)JMO予選の問題 (imojp.org)

これは、いろいろ試していけばわかりますが、数学オリンピックの公式の解答はもっと確実なものなので、そちらを記述しておきます。

下の図のように各マスに数を書き込むと、コインが置かれているマスに書き込まれている数の合計は操作によって増加しないから、置けるマス目の最大値を計算して、置けるコインの枚数の最大値は19であることが分かります。

実際、19枚になる方法を試していけば、答えが、19枚であることが分かります。

数学オリンピックの問題を解けるようになるには

正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか本選の最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。

というわけで、数学オリンピック対策でぜひ読んでおくべき本を紹介したいと思います‼‼

下の記事から抜粋しました。もっと詳しく知りたい方は、ぜひ下の記事を読んでください‼

＼受験生必見‼／数学オリンピックの対策法とは？おすすめの参考書や効率的な勉強法を解説‼

「数学オリンピックを受けようと思ったけど、実際どんなふうに手を付けていったらいいかわからない」と思う方は結構いると思います。なので、今回は数学オリンピックで本選あるいは日本代表やメダリストを目指す上でのオススメ参考書や効率的な勉強法を紹介していきたいと思います‼

information-station.work

パーフェクトマスターシリーズ

これは、特定の分野をしっかり固めたい方にお勧めです。

大事な問題だけがセレクトされているので、その分野の問題をしっかり鍛えることができます。

初等整数を鍛えたい方にオススメ‼‼

これは、初等整数をマスターしたい方にお勧めです。

初等整数の問題はよく本選の大門１なんかで出題されることが多いので、そういった類の問題を解けるようになりたい方はこの本がおすすめです‼‼

平面幾何を鍛えたい方にオススメ‼‼

下の本は平面幾何を鍛えたい方にオススメの本です。

「数学オリンピックの幾何の問題を解いていると、「こんな発想が出てくるわけないだろ！！」みたいな問題にあたることはよくあると思います。

この本を読むことで、そういう問題たちをすらすら解けるようになります‼‼

代数・解析を鍛えたい方にオススメ‼‼

下の本は、代数、解析を鍛えたい方におススメの本です

数学オリンピックの問題の中でも、「絶対解けるか！！」みたいなレベルの問題って稀にあるじゃないですか。

こういう問題は、代数・解析の分野に入ることが多いです。

数学オリンピックで、難しい問題を解いてほかの受験生と差をつけたい方にはこの本をお勧めします‼

組み合わせ論を鍛えたい方にオススメ‼‼

下の本は、組み合わせ論を鍛えたい方におススメの本です。

数学オリンピックの場合の数の問題は、ほかの分野に比べてそこまで難しい問題が出題されることはあまりないんですが、とにかくめちゃくちゃミスしやすいように巧妙に仕組まれています。

そんなミスしやすいポイントをしっかり克服するためにも、ぜひこの本は見ていただきたいです。

過去問をひたすら解きまくる

これも結構おすすめです。過去問を全部解いていれば、実質数学オリンピックに関係する問題を全部網羅したようなものなので、完璧にマスターしたい方にはこちらの方法をお勧めします‼‼

ほかにも過去問についてはいろんな著者がいろんな本を出版しているので、ぜひそちらの本も調べてみてください。

終わりに

いかがでしたか。

最後の4問はやはり難しかったと思います。特に12番は「こんな方法思いつくかー！」というような方法を数学オリンピックは解答として挙げていました。

また、ほかにも数学オリンピックの解説をしている記事がたくさんありますので、カテゴリーや関連記事などからお読みいただければ光栄です。

それでは次の記事で‼