＼超わかりやすい‼／国際数学オリンピック(IMO)2021全問解説‼

初めに

今回は、数学オリンピック2021国際数学オリンピックの問題の解答・解説をしていきたいと思います‼‼

ノーヒントで解いてみたいという方は、下のリンクをクリック‼‼

国際数学オリンピック2021の問題(公式)

また、この記事の最後に、「数学オリンピックの問題を解けるようになる方法」について解説していますので、興味がある方はそちらのほうも読んでいただければ光栄です。

それでは国際数学オリンピック国際数学オリンピック2021の解答・解説を見ていきましょう‼‼

国際数学オリンピック国際数学オリンピック2021　解答・解説　問1

問題：

n≧100を整数とする。康夫君はn,n+1,…,2nをそれぞれ相異なるカードに書き込む。その後、これらのn+1枚のカードをシャッフルし、二つの山に分ける。この時、少なくとも一方の山には、書き込まれた数の和が平方数となるような2枚のカードの組が存在することを示せ。

解答・解説：

この問題を解くことは「カードにある3つの整数で、どの2つの和をとっても平方数」となるようなカードの存在を示すことと同値です。

ここで、正の整数kを用いて、3つの数2k²-4k,2k²+1,2k²+4kが存在したとします。

この時、どの二つの和をとっても平方数となるから、このkの存在を示せばいいことになります。

kが満たす条件は、n≦2k²-4k,かつ,2n≧2k²+4k。つまり、k²+2k≦n≦2k²-4kです。

ここで、nに対して、k²+2k≦nを満たす最大の数をkと定めます。

この時、nが100以上であることは問題文で述べられているため、9*9+2*9≦100より、k≧9であることがわかります。

また、ここで定めたkの定義から、k²+2k≦n<(k+1)²+2(k+1)であることを踏まえて、

2k²+4k-{(k+1)²+2(k+1)}=(k-4)²-19≧6　(k≧9)

より、k²+2k≦n<(k+1)²+2(k+1)<2k²-4kとなります。

よって、kの存在を示すことができたので、これで証明完了です。

国際数学オリンピック国際数学オリンピック2021　解答・解説　問2

問題：

任意の実数\begin{equation*} x_{1} ,…,x_{n} \end{equation*}に対して、不等式

\begin{equation*} \sum\limits _{i=1}^{n}\sum\limits _{j=1}^{n}\sqrt{|x_{i} -x_{j} |} \leqq \sum\limits _{i=1}^{n}\sum\limits _{j=1}^{n}\sqrt{|x_{i} +x_{j} |} \end{equation*}

が成り立つことを示せ。

解答・解説：

数学的帰納法で示していきたいと思います。

当たり前ですけど、n=0,1の時は成立します。

以下、k≧2とし、n=0,1,…,k-1の時は成立していると仮定します。

まず、数列

\begin{equation*} x_{1} ,…,x_{k} \end{equation*}

を任意にとります。

次に、f(t)を

\begin{equation*} f( t) =\sum\limits _{i=1}^{k}\sum\limits _{j=1}^{k}\left(\sqrt{|( x_{i} +t) +( x_{j} +t) |} -\sqrt{|( x_{i} +t) -( x_{j} +t) |}\right) \end{equation*}

と定めます。

ここからが難しいので、ちょっと頑張って理解してください。

上のf(t)の定義式で、第2項のところは、tに関係ないので、定数とみなせます。なので、ここはいったん考えずに行きます。

f(t)の性質について考えてみます。

具体例で考察

ちょっとここからは複雑になってしまうので、具体例を出して、多少理解しやすくしてみようと思います。

問題の数列が、-6,-19,-30だとします。

この時、f(0)=18(左側だけ。)です。

しかし、f(49)≒8.5です。(間違ってたらごめんなさい。)

そして、f(∞)＝∞です。(当たり前ですが…)

何を言いたいかっていうと、単調増加ではないってことです。

グラフをイメージ図で表すと、

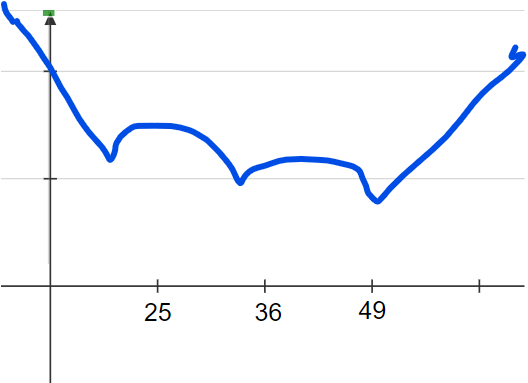
多分こんな感じ。雑過ぎてごめんなさい。

解説の続き

単調増加だとありがたいのになぁと思って解いていたんですが、結局2tとx_iとx_jの和が0になるところがいった沈む場所だとわかったので、(y=√xという上に凸のグラフをいくつ重ねても上に凸になります。)あとは先ほどの和が0になるtで、非負値を取らないことを示せばいいことになります。

ここで、あるi,jに対して、2tとx_iとx_jの和が0になるときのtを小さい順にy₁,…,y_mと置きます。

このとき、f(y₁),…,f(y_m)が非負値を取ることを示せばいいことになります。

• i≠jのとき

2y_n+x_i+x_j=0が成り立っているとします。i=k-1,j=kと置いても一般性は失われないので、ここでは、y_n+x_k＝-(y_n+x_k-1)となる場合を考えればいいことになります。

またこの時、1以上k以下の任意のiに対して、

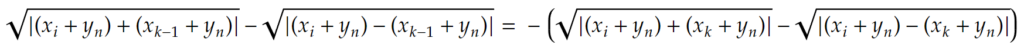
が成り立つため、

\begin{equation*} f( y_{n}) =\sum\limits _{i=1}^{k-1}\sum\limits _{j=1}^{k-1}\left(\sqrt{|( x_{i} +t) +( x_{j} +t) |} -\sqrt{|( x_{i} +t) -( x_{j} +t) |}\right) \end{equation*}

であり、これは帰納法の仮定より、非負です。

• i=jのとき

これも先ほどと同様に、x_k+y_n＝0となる場合を考えればいいことになります。この時、

\begin{equation*} f( y_{n}) =\sum\limits _{i=1}^{k-2}\sum\limits _{j=1}^{k-2}\left(\sqrt{|( x_{i} +t) +( x_{j} +t) |} -\sqrt{|( x_{i} +t) -( x_{j} +t) |}\right) \end{equation*}

であり、これも帰納法の仮定より、非負です。

よって、n=kの時に成り立つことが示され、数学帰納法によってすべてのnに対して題意が満たされることが証明された。

※証明雑くてすみません。もっと詳しく解説してほしい方は、コメント欄で気軽に言ってください！

国際数学オリンピック国際数学オリンピック2021　解答・解説　問3

問題：

DはAB>ACなる鋭角三角形ABCの内部の点であり、∠DAB=∠CADを満たしている。線分AC上の点Eが∠ADE=∠BCDを満たし、線分AB上の点Fが∠FDA＝∠DBCを満たし、直線AC上の点XがCX=BXを満たしている。O₁,O₂をそれぞれ三角形ADC,EXDの外心とする。この時、直線BC,EF,O₁,O₂は一点で交わることを示せ。

解答・解説：

この問題がDay1の中で多分一番難しかったんじゃないかなと思います。

考えてもわからなかったので、公式の解答を写させていただきます。

まず、⊿ABCの点Dに関する等角共役点をQと置きます。(思いつくわけない。)

この時、Dは∠Aを二等分しているので、当たり前ですが、A,D,Qは一直線上にあります。

さらに、∠FDA＝∠CBD=∠FBQより、(左の等号問題の条件,右側の等号は等角共役点の性質。)

下の図にもありますが、F,D,Q,Bは共円です。同様にして、E,D,Q,Cも共円です。

これは結構数学オリンピックに出てくるパターンなんですが、三角形で円二つ出てきたら(語彙力なくてすみません。)方べきの定理で共円がもう一つ現れます。

どういうことかというと、方べきの定理より、AF×AB＝AD×DQ=AE×ACなので、B,F,E,Cも共円です。

これより、∠FEA=∠ABCとなるので、∠DEF+∠BCD＝∠DEF+∠ACQ=∠DEF+∠ADE＝180°－∠EAD－∠FEA＝180°－∠EAD－∠ABC＝(180°－∠DAF－∠FDA)－(∠ABC－∠DBC)＝∠AFD－∠ABD＝∠BDFが成り立ちます。

(↑この変形でわからないところなどあれば気軽にコメント欄で‼)

よって、接弦定理より、赤と青はDで接します。

また、赤と青と緑の根心Tをとります。(数学オリンピックのむずかしい問題では結構出てくるパターンのやつです。)

この時、TD²＝TE×TF＝TC×TBが成り立ちます。

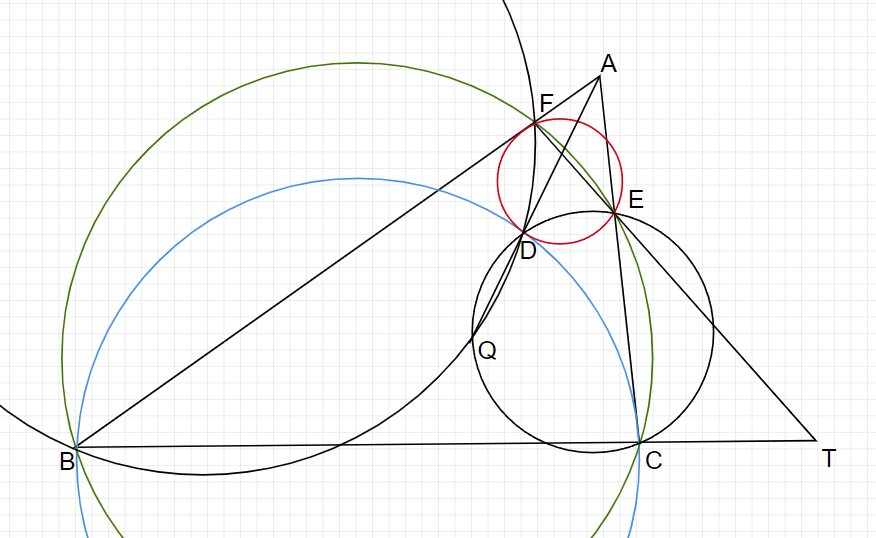
ここでさらに直線ATと三角形ABCの外接円の交点Mを取ると、TC×TB＝TM×TAより、A,F,E,Mは共円と分かります。

で、ここからがこの問題の醍醐味なんですけど、中心T半径TDの円によって、紫の円を反転させます。

円の反転についてはこちら‼

この時、紫色の円(ADCの外接円)を反転させたら、黄色の円(MDBの外接円)が得られます。そして、紫色の円と黄色の円の交点をKとしたとき、TD=TKが成り立ちます。

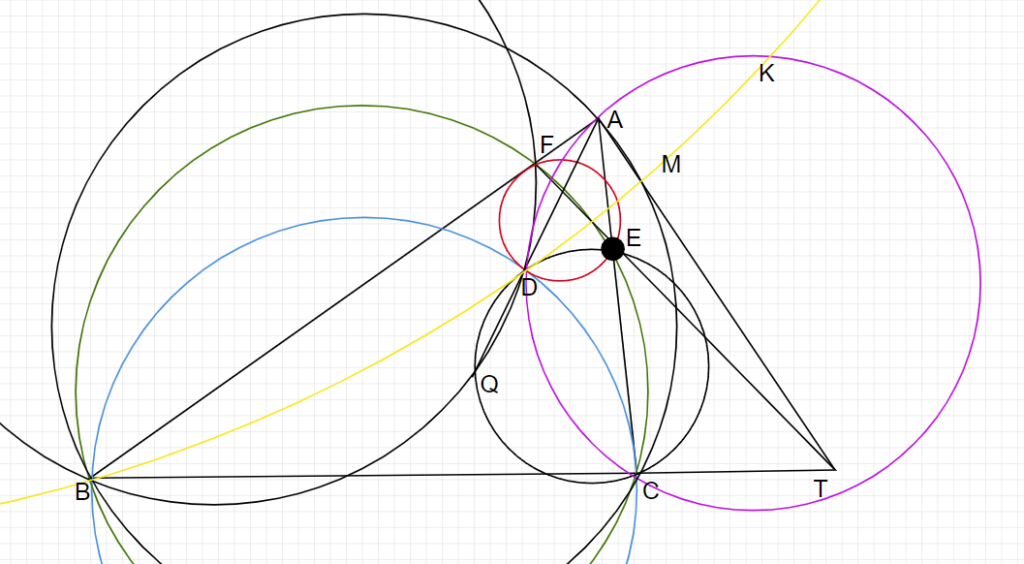
なので、当たり前ですが、オレンジ色の円の外心,紫色の円の外心,TはDKの垂直二等分線上にあります。

ACDの外心はO₁なので、KDEの外心円とEXDの外心円が同一の円であることを示せばいいことになります。

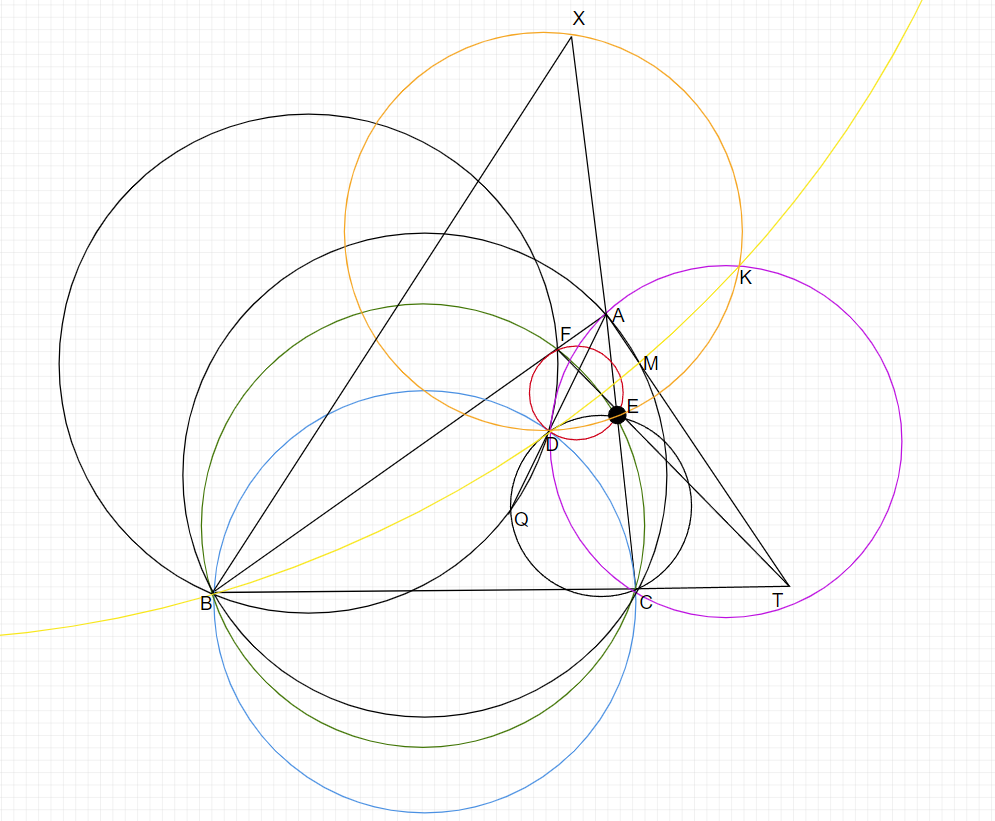
ここで、∠EMB＝∠EMA－∠BMA＝(180°－∠AFE)－∠BCA＝180°－2∠BCA＝∠CXB＝∠EXBであるから、4点B,E,M,Xは同一円周上にあります。

そして、黄色、紫、水色の円の根心を取ると、赤い点になります。

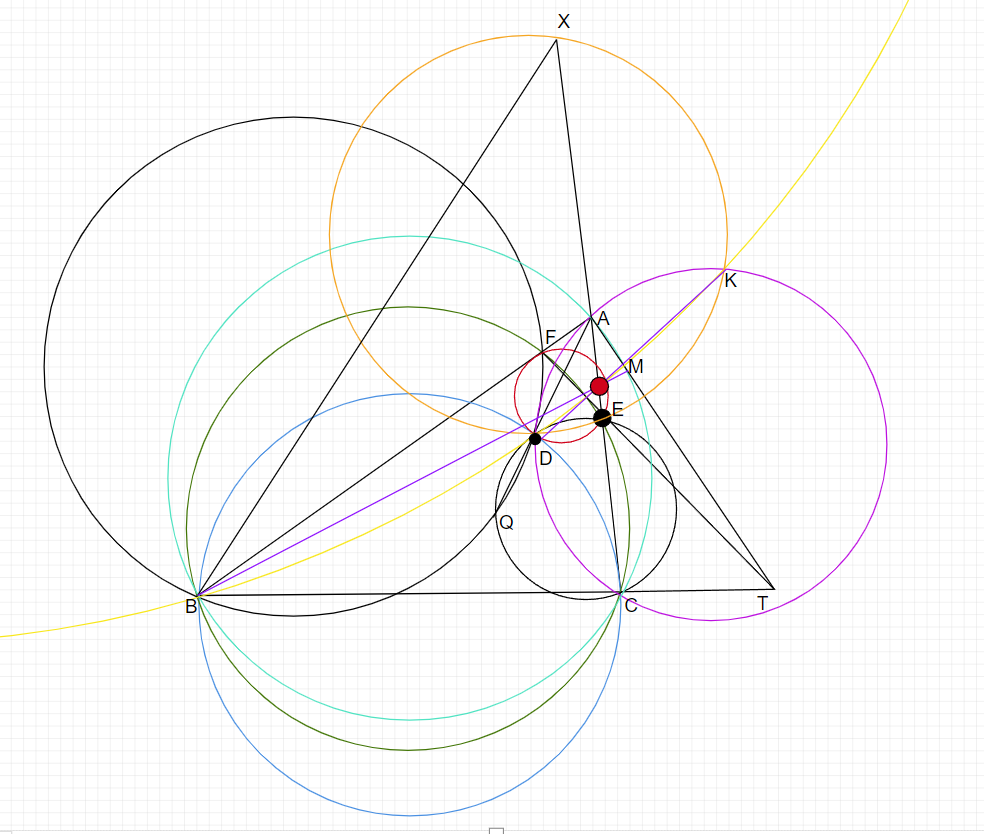
この点をPと置くと、先ほど導いた共円を使って、方べきの定理より、EX・XP＝BM・MP＝DP・KPとなるので、4点D,K,E,Xは同一円周上にあります。

よって、題意は満たされました。

こんな問題解けるわけないですよね。

ただ、

• 根軸
• 円の反転

は数学オリンピックのかなり難しい問題によく出てきます。数学オリンピックで難しい幾何の問題に出会ったらまずはこれを意識してみるのもいいと思います。

国際数学オリンピック国際数学オリンピック2021　解答・解説　問4

問題：

ΓをIを中心とする円とし、凸四角形ABCDの各辺AB,BC,CD,DAがΓに接している。Ωを三角形AICの外接円とする。BAのA側への延長線がΩとXで交わっており、BCのC側への延長線がΩとZで交わっている。また、AD,CDのD側への延長線がそれぞれΩとY,Tで交わっている。この時、

AD+DT+TX+XA=CD+DY+YZ+ZC

が成り立つことを示せ。

解答・解説：

さっきの問題を見た後だと凄い簡単に見えてきますね。

実際、皆さんも初見でワンチャン解けると思います。それぐらいひねりがない問題なので、ぜひ初見で頑張って解いてみてください。(ちなみにDay2で一番簡単なのは5番です。)

それでは解説していきます‼

四角形の各辺がΓと接している点を下のようにP,Q,R,Sと定めて、Ωの中心をOとし、図を描きます。

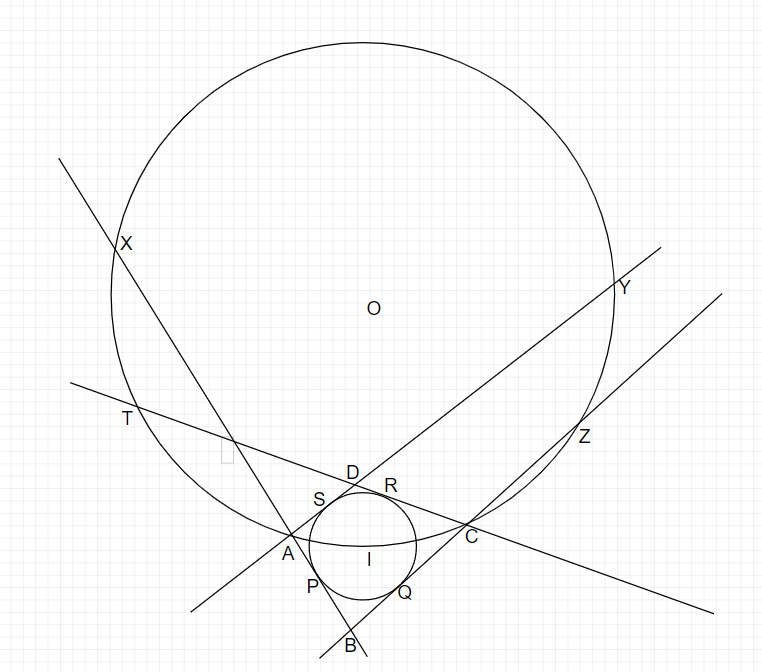
円周角の定理と、円に内接(外接も)する四角形の性質を踏まえると、∠IXY＝∠IAY=∠BAI＝∠XYIとなるため、IX=IYがわかります。同様にIT=IZもわかります。

さらに、対称性より、XT=YZも導かれます。

また、IX=IY,IP=IS,∠IPX＝∠ISY＝∠Rより、直角三角形の合同条件から、⊿IXP≡⊿IYSが導かれます。

これにより、XP=YSが得られます。同様に、RT=QZが得られるので、結局整理すると、

AD+DT+TX+XA=XP+TR+YZ=YS+QZ+YZ=CD+DY+YZ+ZC

となるので、題意は満たされました。

手を動かしてちゃんと図形を分析すれば解けるので、この問題は国際数学オリンピックの2番級にしては非常に簡単だったんじゃないかなと思います。

国際数学オリンピック2021　解答・解説　問5

問題：

2匹のリス,トモとナオは冬を越すために2021個のクルミを集めた。トモはクルミに順に1から2021までの番号を付け、彼らはお気に入りの木の周りに、環状に2021個の穴を掘った。翌朝、トモはナオが番号を気にせずに各穴に1つずつクルミを入れたことに気づいた。仕方がないので、トモは次の操作を2021回行ってクルミを並び替えることにした。k回目の操作では、クルミkと隣り合っている2つのクルミの位置を入れ替える。このとき、あるkが存在して、k回目の操作でトモはa<k<bを満たすクルミa,bを入れ替えることを示せ。

解答・解説：

国際数学オリンピックの問題にしては、かなり簡単な方の問題です。

条件を満たさない並べ方があったとします。

そして、k回目の操作後に番号がk以下のクルミが入っている穴を良い穴とし、それ以外を悪い穴とします。

この時、k回目のときに、クルミkの両隣にあるのはどちらもkより大きいかかどちらもkより小さいかのどちらかになります。

つまり、入れ替える操作によってよい穴と悪い穴は変わらないことになります。また、k回目の操作によってクルミkが入っている穴が悪い穴から良い穴になります。

逆に、それぞれの穴に注目するとk回目の操作によってクルミkが入っていた穴が悪い穴から良い穴に変わり、一度良い穴になったら悪い穴にはならないので、k回目の操作で悪い穴から良い穴に変化する穴にkという番号を与えると、すべての穴には1から2021の番号がちょうど一つずつ割り振られます。

そして、その穴の番号は両隣よりも大きいか、小さいかのどちらかですが、2021は奇数なので、矛盾。

よって題意は満たされました。

国際数学オリンピック2021　解答・解説　問6

問題：

m≧2を整数、Aを(必ずしも正とは限らない)整数からなる有限集合とし、B₁,B₂,…,B_mをAの部分集合とする。各k=1,2,…,mについて、B_kの要素の総和がm^kであるとする。この時、Aは少なくともm/2個の要素を含んでいることを示せ。

解答・解説：

集合Aの要素の数をkとし、その要素をA={a₁,a₂,…,a_k}とし、s(B_i)の要素の総和を表します。ここで、二つの集合

\begin{gather*} C=\left\{\sum\limits _{i=1}^{m} c_{i} s( B_{i}) \ |\ 0\leqq c_{i} \leqq m-1,c_{i} は整数\right\}\\ \\ \end{gather*}

と

\begin{equation*} D=\left\{\sum\limits _{j=1}^{k} d_{j} a_{j} \ |\ 0\leqq d_{j} \leqq m( m-1) ,d_{j} は整数\right\} \end{equation*}

を考えます。

\begin{equation*} s( B_{i}) =\left\{\sum\limits _{j=1}^{k} e_{i,j} a_{j} \ |\ e_{i,j} \in \{0,1\}\right\} \end{equation*}

と書けるので、Cの各要素は

\begin{equation*} \sum\limits _{i=1}^{m} c_{i} s( B_{i}) =\sum\limits _{j=1}^{k}\left(\sum\limits _{i=1}^{m} c_{i} e_{i,j}\right) a_{j} \end{equation*}

と書ける。また、0≦c_i≦m-1(1≦i≦m)より、

\begin{equation*} 0\leqq \sum\limits _{i=1}^{m} c_{i} e_{i,j} \leqq m( m-1) \end{equation*}

であることに注意すると、C⊂Dであることがわかります。

ここで、Cは

\begin{equation*} C=\left\{\sum\limits _{i=1}^{m} c_{i} m^{i} \ |\ 0\leqq c_{i} \leqq m-1,\ c_{i} は整数\right\} \end{equation*}

と書け、m以上m^m+1以下のｍの倍数のm進法での表記を考えるとこれらはすべてＣに含まれることがわかるから、Ｃの要素はm^m個以上であることがわかります。

一方で、Dの要素の数は、(d₁,…,d_k)の組の個数以下なので、{m(m-1)+1}^k個以下です。

m≧2より、m(m-1)+1<m²であるから、m^2k個未満であることがわかります。

よって、m^m<m^2kが導かれるため、

m/2<k

となり、題意は満たされました。

やっぱりこれを初見で解く受験生は凄いですね。かなりの発想力が必要される問題でした。

ほかの大会の問題の記事や、予選とかの問題の解説をしている記事もありますので、そちらの方も見ていただければ嬉しいです。

また、数学オリンピックの問題を解けるようになりたい方は、ぜひ、下のところを読んでください‼‼

数学オリンピックの問題を解けるようになるには

正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか国際数学オリンピックの最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。

というわけで、数学オリンピック対策でぜひ読んでおくべき本を紹介したいと思います‼‼

パーフェクトマスターシリーズ

これは、特定の分野をしっかり固めたい方にお勧めです。

大事な問題だけがセレクトされているので、その分野の問題をしっかり鍛えることができます。

初等整数を鍛えたい方にオススメ‼‼

これは、初等整数をマスターしたい方にお勧めです。

初等整数の問題はよく国際数学オリンピックの大門１なんかで出題されることが多いので、そういった類の問題を解けるようになりたい方はこの本がおすすめです‼‼

平面幾何を鍛えたい方にオススメ‼‼

下の本は平面幾何を鍛えたい方にオススメの本です。

「数学オリンピックの幾何の問題を解いていると、「こんな発想が出てくるわけないだろ！！」みたいな問題にあたることはよくあると思います。

この本を読むことで、そういう問題たちをすらすら解けるようになります‼‼

代数・解析を鍛えたい方にオススメ‼‼

下の本は、代数、解析を鍛えたい方におススメの本です

数学オリンピックの問題の中でも、「絶対解けるか！！」みたいなレベルの問題って稀にあるじゃないですか。

こういう問題は、代数・解析の分野に入ることが多いです。

数学オリンピックで、難しい問題を解いてほかの受験生と差をつけたい方にはこの本をお勧めします‼

組み合わせ論を鍛えたい方にオススメ‼‼

下の本は、組み合わせ論を鍛えたい方におススメの本です。

数学オリンピックの場合の数の問題は、ほかの分野に比べてそこまで難しい問題が出題されることはあまりないんですが、とにかくめちゃくちゃミスしやすいように巧妙に仕組まれています。

そんなミスしやすいポイントをしっかり克服するためにも、ぜひこの本は見ていただきたいです。

過去問をひたすら解きまくる

これも結構おすすめです。過去問を全部解いていれば、実質数学オリンピックに関係する問題を全部網羅したようなものなので、完璧にマスターしたい方にはこちらの方法をお勧めします‼‼

ほかにも過去問についてはいろんな著者がいろんな本を出版しているので、ぜひそちらの本も調べてみてください。(下リンク)

Amazon.com

終わりに

いかがでしたか。

ほかにも数学オリンピックの解説している記事もありますので、そちらのほうも見ていただければ光栄です‼‼

それでは次の記事で‼