初めに
今回は、数学オリンピック2019本選の問題の解答・解説をしていきたいと思います‼‼
ノーヒントで解いてみたいという方は、下のリンクをクリック‼‼
第29回(2019年)JMO本選の問題 (imojp.org)
また、この記事の最後に、「数学オリンピックの問題を解けるようになる方法」について解説していますので、興味がある方はそちらのほうも読んでいただければ光栄です。
それでは日本数学オリンピック本選2019の解答・解説を見ていきましょう‼‼
日本数学オリンピック本選2019 解答・解説 問1
問題:
a2+b+3=(b2-c2)2を満たす正の整数の組(a,b,c)を全て求めよ。
解答・解説:
これは、想像してもらえれば分かりやすいです。
b2-c2がある程度大きくなると、(b=10,c=1とします。) (b2-c2)2 -b-3=992-10-3=9788となり、そもそも一つ下の平方数である、982=9604に届きません。(∴aに入る数がない。)
ということは、b,cに入る数には絶対限界があります。これに注目して解いていきましょう‼
( b2-c2 )2=(|b2-c2|)2の一つ下の平方数は、(|b2-c2|-1)2なので、
(|b2-c2|)2 - (|b2-c2|-1)2 =2 |b2-c2| -1≦b+3
が成り立ちます。この条件は超厳しい条件で、b≠cより、
|b2-c2|=(b+c)|b-c|≧b+1 (b=2、c=1の時)
より、2b+1≦ 2 |b2-c2| -1≦b+3 が導かれるため、
b≦2と分かります。
- b=1の時
a2+4=(c-1)2となり、二つの平方数の差が4となるような整数はないので、不適。
- b=2の時
a2+5=(4-c)2となり、二つの平方数の差が5となるような数の組は、2と3しかありません。よって、この場合は、a=2,c=1です。
よって、もとめる答えは、(a,b,c)=(2,2,1)と分かります。
「二つの平方数の差が4となる数の組はない」とか、「二つの平方数の差が5となる数の組は2と3のみ」とかは証明した方がよさそうですが、解答の流れとしてはこれで大丈夫だと思います。
例年通り問1は簡単でしたね。
日本数学オリンピック本選2019 解答・解説 問2
問題:
nを3以上の奇数とするn×nのマス目を使ってゲームを行う。ゲームはn2ターンからなり、各ターンでは以下の操作を順に行う。
- 整数の書きこまれていないマスを1つ選び、1以上n2以下の整数を一つ書き込む。ゲームを通して度の整数も1回しか書き込めない。
- そのマスを含む行,列それぞれについて,書き込まれている整数の和がnの倍数であれば1点(両方ともnの倍数であれば2点)を得る。
ゲームが終了するまでに得られる点数の総和としてありうる最大の値を求めよ。
解答・解説:
こういう問題は試してみることにつきます。
例えば、5×5の場合を考えます。
5の倍数はおくだけで2点もらえるので、最初に使います。
| 5 | ||||
| 10 | ||||
| 15 | ||||
| 20 | ||||
| 25 |
次に下のように置いたとします。
| 5 | 1 | 4 | ||
| 10 | ||||
| 15 | ||||
| 20 | ||||
| 25 |
この次に、下のように置きます。
| 5 | 1 | 4 | ||
| 10 | 9 | 6 | ||
| 15 | ||||
| 20 | ||||
| 25 |
この時、この操作だけで4点が得られます。なので、これを繰り返したら、25回の操作が終了した後には、30点入ることになります。
これを一般化します。
まず、i行目でj列目のマスを(i,j)とあらわすことにします。このとき、(i,j)≡i+j(mod n)とし、nで割った余りが0をn個、1をn個、n-1をn個…と書き込んでいくとすると、n(n+1)点が得られます。
次に、得られる点数がn(n+1)以下であることを示します。
nの倍数は、一つ置くだけで、最大2点得ることができるので、nの倍数を書き込むことで得ることができる最大の点数は2点です。
また、nの倍数以外については、行がnの倍数になって1点を得るためには、最低でも2つ書き込まないといけません。
なので、nの倍数以外を書き込むことで、行がnの倍数になって得られる点数の合計の最大は、nが奇数であることから、(n-1)n/2点です。
これは列についてもいえるので、nの倍数以外の数を書き込むことによって得られる点数の合計は、(n-1)n点と分かります。
よって、得られる点数としてあり得る最大の値は、n(n-1)+2n=n(n+1)点であり、n(n+1)点が得られるような書き込み方は先ほど示した通り存在するので、もとめる答えは、n(n+1)点であることがわかります。
日本数学オリンピック本選2019 解答・解説 問3
問題:
世の実数に対して定義され、正の実数とる関数fであって、任意の正の実数x,yに対して、
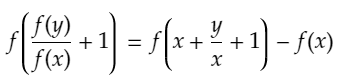
が成り立つものを全て求めよ。
解答・解説:
「どうせ数学オリンピックのことだし、f(x)=xが答えでしょ…」と思ってやってみます。
確かに、f(x)=xとすると成り立ちます。
さらに、f(x)=2xとしても成り立ちます。もしかして…と思い、f(x)=axとしてみても、やっぱり成り立ちます。
というわけで、f(x)=~xという形を目指して解いていきます。
そのためには、まず、fが単射であることを示します。
s>t>0,f(s)=f(t)とします。今使える条件は、x=yとしたときの、f(x+2)-f(x)=f(2)>0ぐらいしかないので、これを頑張って生かそうと考えます。
y=s,tを代入した時、(xに代入すると、計算がめんどくさくなるからです。)
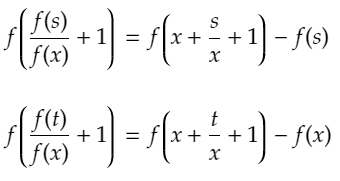
となります。なので、x=(1/2)(s-t)とすると、
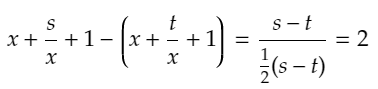
となり、左辺は同じなのに、右辺の値が違うため、矛盾します。
よって、fは単射であることがわかります。
なので、x=2を代入して、
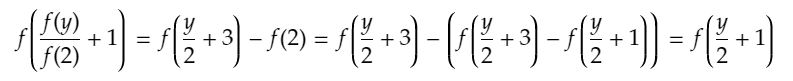
が得られ、fが単射であることから、
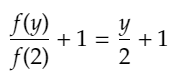
が得られます。
よって、f(y)={f(2)/2}yより、fは、正の実数aを使って、f(x)=axとあらわすことが導かれます。
今年の3番は例年に比べたらややマシだったかなと思います。
特に、私のように答えの予想ができてたらこの証明の流れは自然だと思うので、簡単に解くことができます。
日本数学オリンピック本選2019 解答・解説 問4
問題:
三角形ABCの内心をI、内接円をωとする。また、辺BCの中点をMとする。点Aを通り、直線BCに垂直な直線と、点Mを通り、直線AIに垂直な直線の交点をKとするとき、線分AKを直径とする円はωに接することを示せ。
解答・解説:
全くわかりませんでした。
なので、下のような本に乗っている公式の解答を写させてもらいます。
まずは、図を描いていきます。
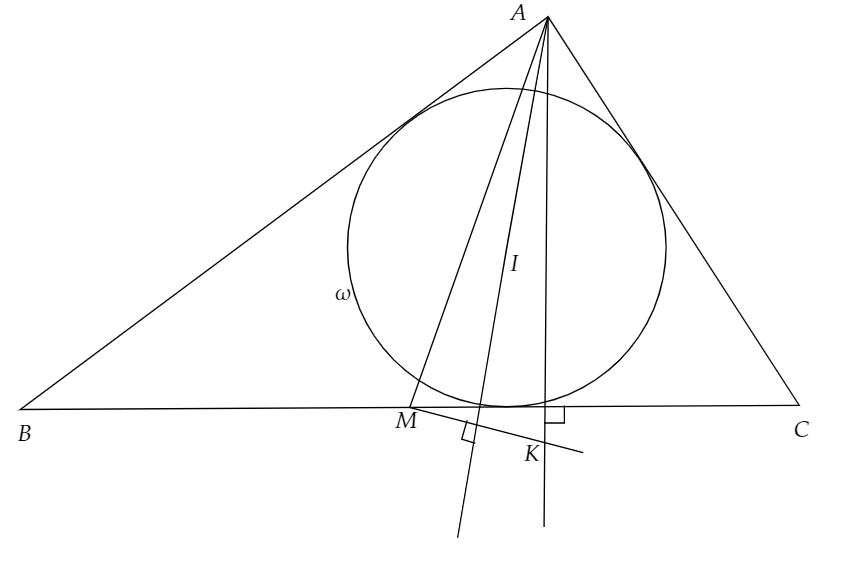
ωとBCの接点をDとし、また、線分DD‘がωの直径となるように点D‘を取ります。さらに、∠A内の傍接円をΩとし、ΩとBCの交点をEとし、線分EE‘がΩの直径となるように点E‘を取ります。また、直線AD‘とωのD‘以外の交点をFとし、直線AE‘とΩのE‘以外の交点をGとします。
図で表すと、めちゃくちゃややこしいですが、下のようになります。
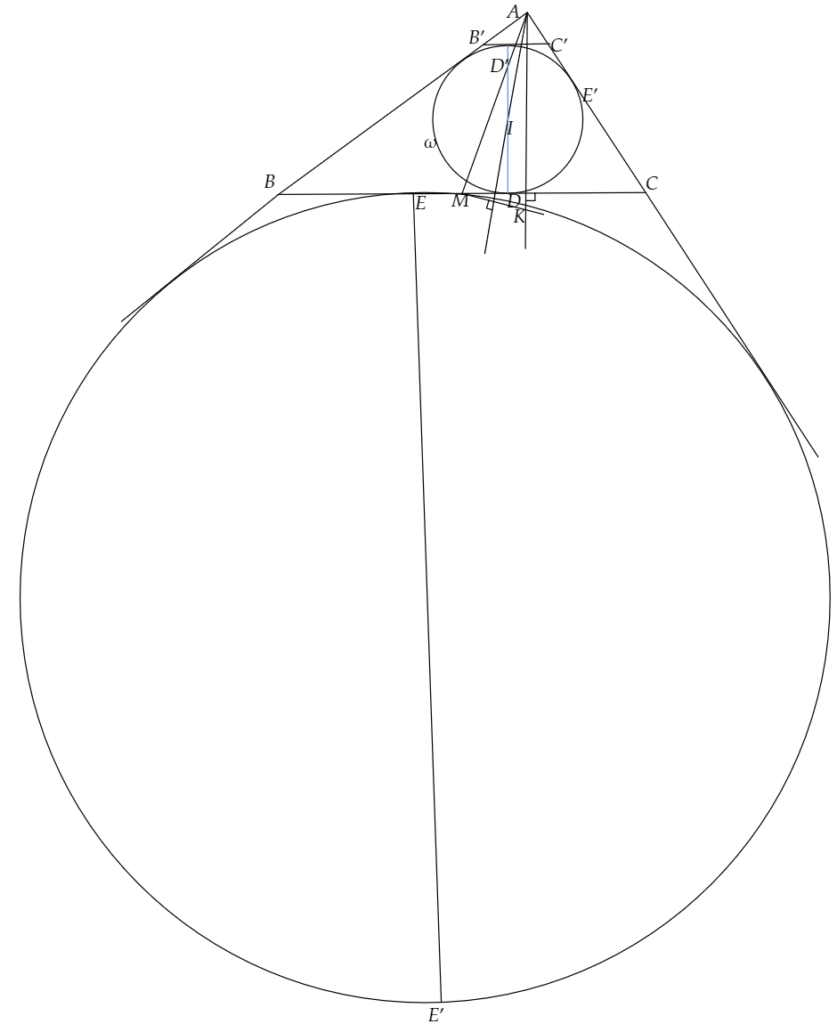
そして、上のようにD’を通るΩの接線と直線AB、ACの交点をそれぞれB’,C’とすると、直線BCと直線B’C’が平行であることから、⊿ABC∽⊿AB’C’において、D’とEは対応しています。(どちらも∠A内の傍接円だから。)
よって、A,D’,E’は一直線上にあることがわかります。
また、DD’がωの直径であることから、∠DFD’=90°であることがわかり、これにより、先ほど導いたことから、∠DFE=90°であることがわかります。
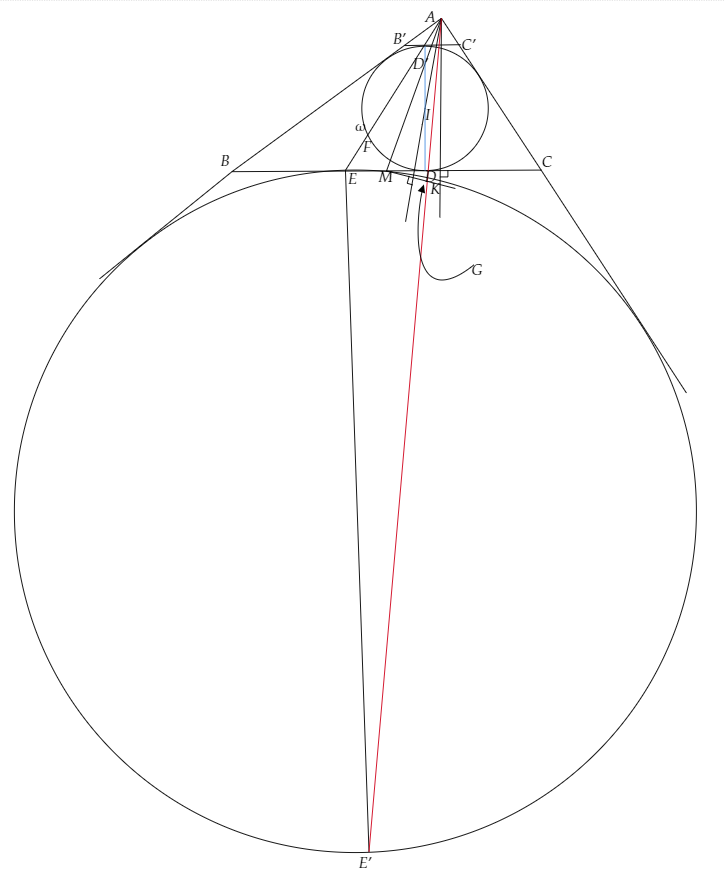
よって、DFとEGの交点をK’とすると、K’は三角形ADEの垂心となるため、BCとAK’は垂直であることがわかります。
ここで、ωが三角形ABCに内接していることから、BD=(1/2)(AB+BC-CA)であり、Ωが三角形ABCの傍接円であることから、AB+BC-CE=CE+ACとなるので、BD=CEより、Mは線分DEの中点と分かります。
したがって、Mにおける2円ω,Ωの方べきの値は同じです。
また、先ほど導いた90°を使うと、D,E,F,Gは円周上にあることがわかります。よって、方べきの定理より、K’D×K’F=K’E×K’Gが成り立ちます。
なので、K’においても、ωとΩの方べきの値は等しいです。
よって、Ωの中心をIAとすると、内接円と傍接円の関係より、A,I,IAは同一直線上にあり、MK’は、ωとΩの根軸となります。(こんなん思いつくかー)
これにより、MK’は、AIに垂直であることがわかります。
以上のことから、長くなりましたが、K’とKは一致することがわかるため、K,D,Fは一直線上にあることがわかります。
よって、DD’//AKより、FKA∽FDD’であり、∠AFK=90°より、FKAの外接円とAKを直径とする円は同一であることがわかり、ωとAKを直径とする円はFで接することがわかるため、題意は満たされました。
めちゃくちゃ難しかったですね。
特に、根軸を持ち出してくるという発想がなかなかないと思います。
フォイエルバッハの定理の初等幾何における証明方法を知っていた人なら、この問題を普通に解けたかもしれません。
日本数学オリンピック本選2019 解答・解説 問5
問題:
正の整数からなる集合Sについて、どの相異なるSの要素x,y,zについてもそれらのうち少なくとも一つはx+y+zであるときSは美しい集合であるという。以下の条件を満たす整数Nが存在することを示し、そのようなXのうち最小のものを求めよ。
- 任意の美しい集合Sについて、2以上の整数nSであって、nSの倍数でないSの要素の個数がN以下であるようなものが存在する。
解答・解説:
このレベルの問題になってくると、出題者側はもう解かせる気がないといっていいぐらい難しいです。
考えてもわからなかったので、数学オリンピックの公式の解答(下の本)を見ることに…
答えを見たら、「あー」とはなりますが、「どっからその発想出てくるんだよ!」ってレベルだったので、この問題を初見で解いた受験生がもしいたら本当に尊敬します。
証明
まず、美しい集合のうち、どの異なる二つの要素も互いに素であるようなものをとても美しい集合と呼びます。
また、以下では整数x,yについてxがyで割り切れることを、y | xとあらわします。
まず、5以下の場合は成立しないことを証明します。
3以上の互いに素である二つの奇数をそれぞれ、a1,a2とします。この時、中国剰余定理より、
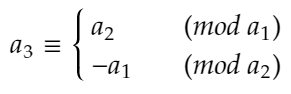
となる3以上の奇数a3を取ることができます。同様にして、3以上の奇数a4,a5を下のようにとることができます。
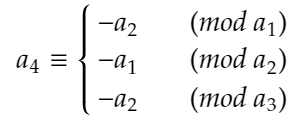
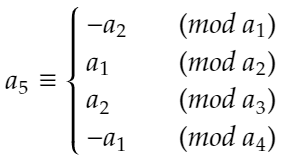
また、a1,a2,a3,a4,a5はそれぞれ互いに素であることから、 S={1,2, a1,a2,a3,a4,a5 }は、美しい集合であることがわかります。
しかし、この時、N≦5だとすると問題の条件を満たさないのでN≧6と分かります。
※私もここまではいけました。数学オリンピックの問題で、「互いに素」が来たら、大体、オイラーの定理か、フェルマーの小定理か、中国の剰余定理ぐらいしかないので、これを知ってたらここまでは誰でも余裕で行けます。
ここで、簡単な補題を3つ証明しておきます。
試行錯誤していっていたら簡単にわかることなので、別にわかっている方はこの部分は読み飛ばしていただいて結構です‼
補題1
正の整数x,y,zが、x<z,y<z,z | x+y+zを満たすとき、z=x+y
補題1の証明
これは証明しようがないというか…常識というか…当たり前すぎるというか…“補題”と呼んでいいのか…
x+y=2zとすると、絶対xかyのどっちかがzより大きくなってしまうため、題意は満たされました。
補題2
正の奇数x,y,zが、x<z,y<z,z | x+y+zを満たすことはない。
補題2の証明
これも世間の常識です。補題1より自明としか言いようがありません。
補題3
Sを一つも偶数を含まないとても美しい集合とする。x,yはx<yを満たすSの要素とするとき、xよりも小さいSの要素zであって、x+yを割り切らないものは高々1個である。
補題3の証明
この補題が思いつくかどうかはさておきとして、この補題自体の証明はそこまで難しいわけではないです。
zをxよりも小さいSの要素とするとき、x,y,zはz<x<yを満たす奇数です。
しかし補題2より、y | x+y+zとなることはないので、x | x+y+zまたはz | x+y+zであることがわかります。
ここで、xよりも小さいSの要素zであって、x+yを割り切らないものが二つ以上あるとします。
このとき、その二つをそれぞれα、βとすると、(α+y)-(a+β)=α-βはxで割り切れるが、この値はxより小さいので、題意は満たされました。
これで、3つの補題の証明は完了です。
証明の続き
3つ(実質一つ)の補題の証明が終わったので、証明の続きをしていきます。
ここで、とても美しい集合の要素の個数が高々7であることを示そうと思います。
とても美しい集合の要素の個数が高々7個であることの証明
偶数は高々一つしか含まれないので、1も偶数も含まれないようなとても美しい集合の要素が5個以下であることを示せばいいことがわかります。
ここで、要素の個数が6個であるとし、それらを小さいほうから、x1,x2,x3,x4,x5,x6とします。
また、下のようにy4,y5,y6を取ります。
y4= x5+x6 y5=x4+x6 y6=x4+x6
k=1,2,3として、xkが、y4,y5,y6を3つとも割り切ると仮定すると、 xkが、2x4=-y4+y5+y6 も割り切ることになってしまうので、互いに素であることに矛盾します。
また、補題3より、 i=4,5,6について、xkがyiを割り切るようなkは2個以上あることがわかります。
よって、 xkがyiを割り切るようなk,lの組は、k=1,2,3と補題3より、ちょうど6個であることがわかるため、各 yiについてそれを割り切ることができるxkの個数はちょうど2個ずつに分けられることがわかります。
さらに、補題3より、 y4は、x1,x2,x3,x4のうちの3つ以上で割り切れることがわかります。
よって、先ほど分かったことから、 y4 はx4で割り切れることがわかります。
ここで、xkのうち y5 を割り切らないものを xm , y6を割り切らないものをxnとすると、補題2より、 x4 | x5+xm , x4 | x6+xn が成り立つため、xn+xm=(x5+xm)+(x6+xn)‐y4もx4で割り切れることになります。
しかし、これは補題2に矛盾しています。
よって、とても美しい集合の要素の数は高々7個であることが証明されました。
証明の詰め
先ほどのことから、Sがとても美しい集合の場合は要素数が7以下であり、nS=2とすると、nSの倍数でない要素は6個以下しかないとわかります。
次に、Sがとても美しい集合でないとします。
正の整数の組nについて、Sがn個以上の要素を持つとき、Sの要素のうち小さいほうからn番目までの要素からなる集合を Snと置くことにします。
先ほどのことから、 Snがとても美しい集合ではないような最小のnを取ると、Snの要素の数は8個以下であることがわかります。
この時、ある素数pが存在して、 Snの要素のうち二つを割り切るため、これらの要素をa,bとします。
mがSnに含まれないSの要素であるとき、a,b,mに注目すると、
- a | a+b+mまたはb | a+b+mのとき、p | mとなります。
- m | a+b+mのとき、補題1より、m=a+bとなるので、p | mとなります。
よって、nS=pとすると、nSの倍数でないSの要素は、a,b以外の Snの要素のみなので、これらは8-2で6個以下しかありません。
以上のことから、N=6は条件を満たし、これが条件を満たす最小の整数です。
この問題、ここ数年の中でも、結構難しいほうだと思います。
これを初見で解ける受験生がいたら普通にすごいと思います。
これで、問題の解説は終了です。
ほかの年の問題の記事や、予選とかの問題の解説をしている記事もありますので、そちらの方も見ていただければ嬉しいです。
また、数学オリンピックの問題を解けるようになりたい方は、ぜひ、下のところを読んでください‼‼
数学オリンピックの問題を解けるようになるには
正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか本選の最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。
というわけで、数学オリンピック対策でぜひ読んでおくべき本を紹介したいと思います‼‼
パーフェクトマスターシリーズ
これは、特定の分野をしっかり固めたい方にお勧めです。
大事な問題だけがセレクトされているので、その分野の問題をしっかり鍛えることができます。
初等整数を鍛えたい方にオススメ‼‼
これは、初等整数をマスターしたい方にお勧めです。
初等整数の問題はよく本選の大門1なんかで出題されることが多いので、そういった類の問題を解けるようになりたい方はこの本がおすすめです‼‼
平面幾何を鍛えたい方にオススメ‼‼
下の本は平面幾何を鍛えたい方にオススメの本です。
「数学オリンピックの幾何の問題を解いていると、「こんな発想が出てくるわけないだろ!!」みたいな問題にあたることはよくあると思います。
この本を読むことで、そういう問題たちをすらすら解けるようになります‼‼
代数・解析を鍛えたい方にオススメ‼‼
下の本は、代数、解析を鍛えたい方におススメの本です
数学オリンピックの問題の中でも、「絶対解けるか!!」みたいなレベルの問題って稀にあるじゃないですか。
こういう問題は、代数・解析の分野に入ることが多いです。
数学オリンピックで、難しい問題を解いてほかの受験生と差をつけたい方にはこの本をお勧めします‼
組み合わせ論を鍛えたい方にオススメ‼‼
下の本は、組み合わせ論を鍛えたい方におススメの本です。
数学オリンピックの場合の数の問題は、ほかの分野に比べてそこまで難しい問題が出題されることはあまりないんですが、とにかくめちゃくちゃミスしやすいように巧妙に仕組まれています。
そんなミスしやすいポイントをしっかり克服するためにも、ぜひこの本は見ていただきたいです。
過去問をひたすら解きまくる
これも結構おすすめです。過去問を全部解いていれば、実質数学オリンピックに関係する問題を全部網羅したようなものなので、完璧にマスターしたい方にはこちらの方法をお勧めします‼‼
ほかにも過去問についてはいろんな著者がいろんな本を出版しているので、ぜひそちらの本も調べてみてください。(下リンク)
数学オリンピックの参考書は高すぎる‼‼
今紹介させていただいた本を見て思ったかもしれませんが、とにかくこういった類の参考書は高いです。
でも、なんと「kindle Unlimited」なら、今紹介した本が月額980円払うだけでで読むことができます‼‼‼
1冊読むだけで余裕で元を取れますね。
さらに、今だけ初月無料なので、初月だけ契約すれば、本当に1銭も払わず、あの高額な本たちを読むことができます😎
私もこれを使っていて、「kindle Unlimited」なら、大体の本が無料で読めちゃうので、知りたいことがあったら簡単に本で調べたり、本で勉強したりすることができます。
また、息抜きに読書したいときにも役に立つので、ぜひこれは、お勧めしたいです‼‼
↓興味がある方はこちら‼‼
終わりに
いかがでしたか。
ほかにも数学オリンピックの解説している記事もありますので、そちらのほうも見ていただければ光栄です‼‼
それでは次の記事で‼
プロフィール
このブログの情報が少しでも役に立てれば嬉しいです。