初めに
今回は、数学オリンピック2018予選の問題の解答・解説をしていきたいと思います‼‼
ノーヒントで解いてみたいという方は、下のリンクをクリック‼‼
第28回(2018年)JMO予選の問題 (imojp.org)
また、この記事の最後に、「数学オリンピックの問題を解けるようになる方法」について解説していますので、興味がある方はそちらのほうも読んでいただければ光栄です。
注意
この記事では、日本数学オリンピック予選2018の問題のうち、問5から問8までしかしていません。
ほかの問題の解答・解説が気になる方は、下のリンクをクリック‼‼
それでは日本数学オリンピック予選2018の解答・解説を見ていきましょう‼‼
日本数学オリンピック予選2018 解答・解説 問5
問題:
11個のオセロの石が一列に(a)のようにならんでいる。次のように裏返すことを何回か行う。:
- 表の色が同じで隣り合わない2つの石であって、その間にはもう一方の石しかないものを選ぶ。そしてその間の石を全て同時に裏返す。
この時、(b)のようになるまでの裏返し方は何通りあるか。

解答・解説:
最初に裏返す駒の選び方は9通り、次に裏返す駒の選び方は7通り、という風になっていくので、もとめる答えは、
9×7×5×3=945
より、945通りであることがわかります。
日本数学オリンピック予選2018 解答・解説 問6
問題:
三角形ABCは直角二等辺三角形で、∠A=90°である。その内部に3点X,Y,Zをとったところ、三角形XYZは∠X=90°であるような直角二等辺三角形であり、さらに3点A,Y,Xおよび、B,Z,YおよびC,X,Zはそれぞれこの順に同一直線上に並んでいた。AB=1,XY=1/4の時、線分AXの長さを求めよ。ただし、STで線分STの長さを表すものとする。
解答・解説:
図を描くと下のようになります。
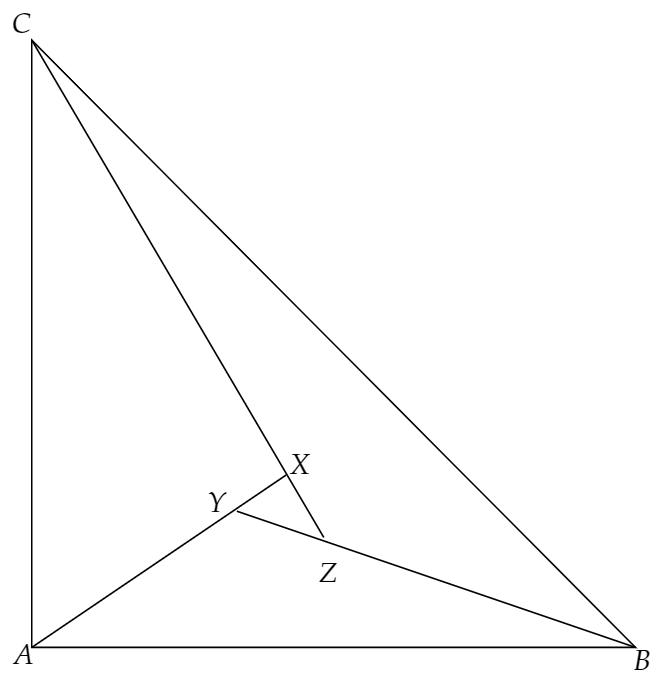
ここで、AX=PXとなるように下のように点Pを取り、APを結びます。
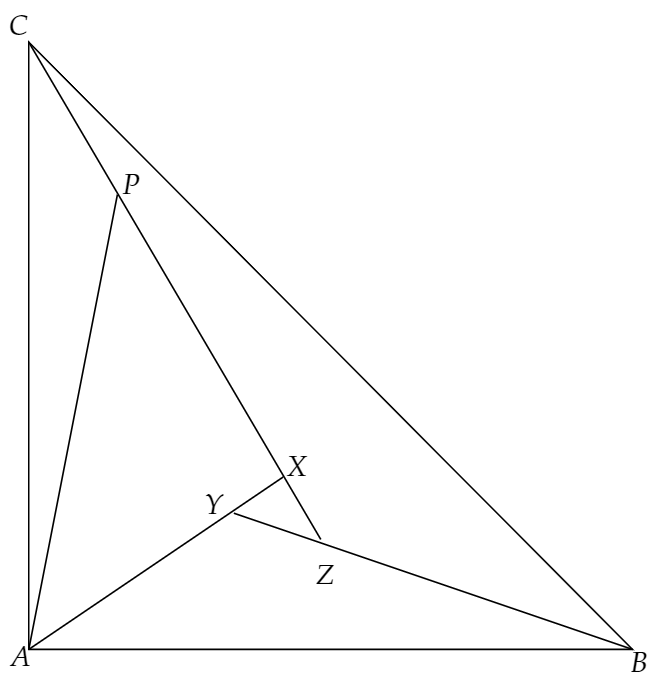
この時、角度を見てもらうと、⊿ACP∽⊿CBZであり、相似比は1:√2であることがわかります。
よって、もとめるAX=kと置くと、CZ=√2×√2×k=2kであることから、⊿AXCに注目して、三平方の定理より、
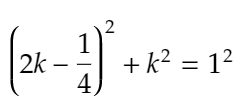
が導かれるので、これを解くことで、
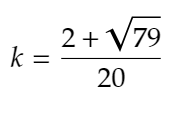
がわかるため、もとめるAXの長さは、
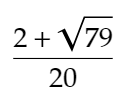
とわかります。
日本数学オリンピック予選2018 解答・解説 問7
問題:
1以上12以下の整数を2個ずつ、6個のペアに分割する。iとjがペアになっているとき、|i-j|の値をそのペアの得点とする。6組のペアの得点の総和が30となるような分割の方法は何通りあるか。
解答・解説:
当たり前ですが、i>jのときは、|i-j|=i-jであり、i≦jのときは、|i-j|=j-iです。
なので、これも当たり前ですが、6組のペアの絶対値を全部外して足し合わせたものは、絶対に、「正のもの」が6個,「負のもの」が6個となります。
なので、1から12までの総和は78ですから、(78-30)÷2=24より、先ほどの「負のもの」の合計は、24であることがわかります。
このような6個の数の選び方は、1から6までの総和が21であることから、これを少しいじることで、(1,2,3,4,5,6+3),(1,2,3,4,5+3,6)=(1,2,3,4,5+1,6+2),(1,2,3,4+3,5,6)の3つであることがわかります。
それぞれの場合について考えていきます。
- 負のものが(1,2,3,4,5,6+3)のとき
9とくっつくのが10,11,12のどれかであればいいので、(もし9とくっつくものが9より小さかったとすると、9が正のものになってしまいます。)この場合における通り数は、3×5!=360より、360通りと分かります。
- 負のものが(1,2,3,4,6,8)のとき
6とくっつくのが5ではなく、8とくっつくのが9以上であればいいため、この場合における通り数は、4×4×4!=386より、386通りであることがわかります。
- 負のものが(1,2,3,5,6,7)のとき
5,6,7が4とくっつかなければいいので、この場合における通り数は、5×4×3×3!=360より、360通りと分かります。
よって、以上から、もとめる答えは、360+384+360=1104より、1104通りと分かります。
日本数学オリンピック予選2018 解答・解説 問8
問題:
a1,a2…a6およびb1,b2…b6およびc1,c2…c6がそれぞれ1,2,3,4,5,6の並べ替えであるとき、
a1b1+a2b2+…+a6b6+b1c1+b2c2+…+b6c6+c1a1+c2a2+…+c6a6
のとりうる最小の値を求めよ。
解答・解説:
まず、問題の式は下のように変形を施すことができます。
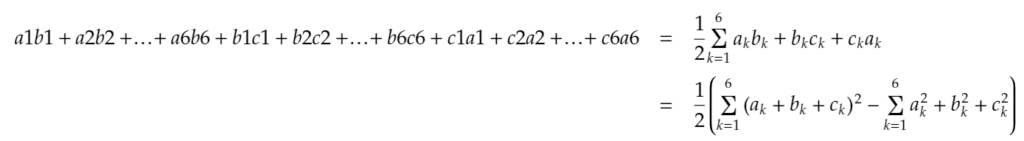
ここで、二番目の項の値は、「a1,a2…a6およびb1,b2…b6およびc1,c2…c6がそれぞれ1,2,3,4,5,6の並べ替え」であることから、さらに下のように変形することができます。
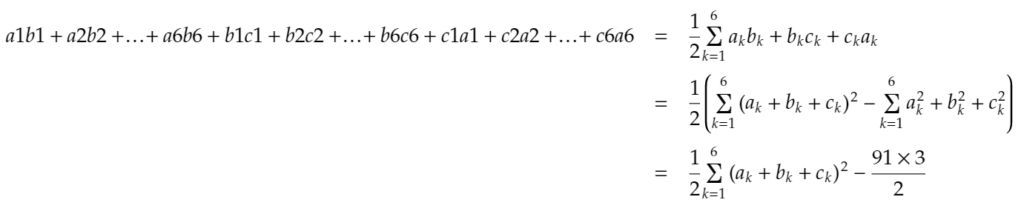
よって、上の式の第1項のところの最小値を求めればいいとわかります。
ここで、いったんakとかの概念を忘れます。
そして、「和が63(a,b,cすべての和)となるような6個の整数で、それぞれを2乗したものの最小値はいくつになるか」という問題を考えます。
当たり前(?)ですが、和が一定の時はそれぞれの数はできるだけに多様な値にした方が値は小さくなります。
例えば、和が10となるような正整数の組で、それぞれの2乗を足したものを考えると、下のように5と5になったときに一番値が小さくなります。
| 分け方 | 1,9 | 2,8 | 3,7 | 4,6 | 5,5 |
| 上で分けた二つの数をそれぞれ2乗して足したものの値 | 82 | 68 | 58 | 52 | 50 |
だから、多分先ほどの問題で最小となる分け方は、(10,10,10,11,11,11)であることが簡単に推測できます。(できるだけそれぞれの値が近くなるようにするため。)
一応証明しておきます。
上の(10,10,10,11,11,11)から、任意の数(s)に1を足して、s以外の任意の数(t)からは1を引きます。(|s-t|≦1となります。)
この時、
(s+1)2+(t-1)2-s2-t2=2s-2t+2≧0
となるため、(10,10,10,11,11,11)の中の任意の数に1を足して、それ以外の任意の数から1を引いたもので値を求める必ず(10,10,10,11,11,11)の時の値以上になることがわかります。
また、「任意の数に1を足して、それ以外の任意の数から1を引く」という動作を繰り返すことで、すべての分け方にたどり着くことができるので、(10,10,10,11,11,11)の最小性が導かれました。
次に、「(10,10,10,11,11,11)となるようにa,b,cを取ることができるのか」という話ですが、例えば、下のように分けることで、これを満たすa,b,cの組み合わせは存在します。
| a | b | c | 和 |
| 1 | 4 | 5 | 10 |
| 2 | 5 | 3 | 10 |
| 3 | 1 | 6 | 10 |
| 4 | 6 | 1 | 11 |
| 5 | 2 | 4 | 11 |
| 6 | 3 | 2 | 11 |
よって、もとめる最小値は、
((100+121)×3-91×3)/2=195
より、195と分かります。
数学オリンピックの問題を解けるようになるには
正直言って、数学オリンピックの問題ぐらいだったら(国際数学オリンピックの最終問題とか本選の最終問題とかを除いて)大体パターン化されているので、勉強さえしておいたら何とかなります。
というわけで、数学オリンピック対策でぜひ読んでおくべき本を紹介したいと思います‼‼
パーフェクトマスターシリーズ
これは、特定の分野をしっかり固めたい方にお勧めです。
大事な問題だけがセレクトされているので、その分野の問題をしっかり鍛えることができます。
初等整数を鍛えたい方にオススメ‼‼
これは、初等整数をマスターしたい方にお勧めです。
初等整数の問題はよく本選の大門1なんかで出題されることが多いので、そういった類の問題を解けるようになりたい方はこの本がおすすめです‼‼

平面幾何を鍛えたい方にオススメ‼‼
下の本は平面幾何を鍛えたい方にオススメの本です。
「数学オリンピックの幾何の問題を解いていると、「こんな発想が出てくるわけないだろ!!」みたいな問題にあたることはよくあると思います。
この本を読むことで、そういう問題たちをすらすら解けるようになります‼‼

代数・解析を鍛えたい方にオススメ‼‼
下の本は、代数、解析を鍛えたい方におススメの本です
数学オリンピックの問題の中でも、「絶対解けるか!!」みたいなレベルの問題って稀にあるじゃないですか。
こういう問題は、代数・解析の分野に入ることが多いです。
数学オリンピックで、難しい問題を解いてほかの受験生と差をつけたい方にはこの本をお勧めします‼

組み合わせ論を鍛えたい方にオススメ‼‼
下の本は、組み合わせ論を鍛えたい方におススメの本です。
数学オリンピックの場合の数の問題は、ほかの分野に比べてそこまで難しい問題が出題されることはあまりないんですが、とにかくめちゃくちゃミスしやすいように巧妙に仕組まれています。
そんなミスしやすいポイントをしっかり克服するためにも、ぜひこの本は見ていただきたいです。

過去問をひたすら解きまくる
これも結構おすすめです。過去問を全部解いていれば、実質数学オリンピックに関係する問題を全部網羅したようなものなので、完璧にマスターしたい方にはこちらの方法をお勧めします‼‼


ほかにも過去問についてはいろんな著者がいろんな本を出版しているので、ぜひそちらの本も調べてみてください。(下リンク)
数学オリンピックの参考書は高すぎる‼‼
今紹介させていただいた本を見て思ったかもしれませんが、とにかくこういった類の参考書は高いです。
でも、なんと「kindle Unlimited」なら、今紹介した本が月額980円払うだけでで読むことができます‼‼‼
1冊読むだけで余裕で元を取れますね。
さらに、今だけ初月無料なので、初月だけ契約すれば、本当に1銭も払わず、あの高額な本たちを読むことができます😎
私もこれを使っていて、「kindle Unlimited」なら、大体の本が無料で読めちゃうので、知りたいことがあったら簡単に本で調べたり、本で勉強したりすることができます。
また、息抜きに読書したいときにも役に立つので、ぜひこれは、使ってほしいです‼
↓興味がある方はこちら‼‼
終わりに
いかがでしたか。
ほかにも数学オリンピックの解説している記事もありますので、そちらのほうも見ていただければ光栄です‼‼
それでは次の記事で‼


プロフィール
このブログの情報が少しでも役に立てれば嬉しいです。